การแก้สมการโดยวิธีการอย่างง่ายจะช่วยให้เราหาผลเฉลยของสมการกำลังสองเท่านั้น
สำหรับการแก้สมการพหุนามนั้น จำเป็นต้องอาศัยทฤษฎีบทเศษเหลือเข้าช่วยด้วยนะครับ

ทฤษฎีบท

ให้ p(x) คือ พหุนาม anxn+ an-1xn-1+ ... +a1x + a0

โดยที่ n เป็นจำนวนเต็ม และ an, an-1, ..., a1, a0เป็นจำนวนจริง

ซึ่ง an≠ 0 จะได้

1. ถ้าหาร p(x) ด้วย (x - c) จะเหลือเศษเท่ากับ p(c) เสมอ

2. ถ้า p(c) = 0 แล้ว (x - c) จะเป็นตัวประกอบของ p(x)

การแยกตัวประกอบโดยใช้ทฤษฏีบทเศษเหลือ

ในที่นี้จะแบ่งออกเป็น 2 กรณีนะครับ นั่นคือ กรณีที่ an= 1 และ an≠ 1

เรามาดูกรณีแรกกันก่อนเลยนะครับ

ถ้าan= 1เราจะหา (x-c) ที่เป็นตัวประกอบของ p(x) ได้โดย

1. เลือกค่า c ที่ทำให้ p(c) = 0 โดยที่ c คือ ตัวประกอบบางตัวของ a0

2. นำ (x-c) ไปหาร p(x) ผลหารที่ได้ คือ q(x)

3. ถ้า q(x) ที่ได้ มีดีกรีเท่ากับ 2 ให้ทำการแยกตัวประกอบของ q(x) ออกเป็น 2 วงเล็บได้เลยครับ

4. แต่ถ้ามากกว่า 2 ให้ทำซ้ำตั้งแต่ข้อ 1-3 อีกครั้งนะครับ จนกว่าจะได้ดีกรีเท่ากับ 2 ครับ

ส่วนอีกกรณี คือan≠ 1เราจะหา (x-c) ได้ดังนี้นะครับ

1. ให้เลือกค่าของ c = k/m ที่ทำให้ p(c) = 0 เมื่อ k คือ ตัวประกอบบางตัวของ a0และ m คือ ตัวประกอบบางตัวของ anโดยที่ ห.ร.ม.ของ k, m คือ 1

2. จากนั้นนำ x(c) ไปหาร p(x) จะได้ผลหารคือ q(x) แล้วจึงแยกตัวประกอบของ q(x) ตามวิธีเดียวกับข้อกรณีแรกนะครับ

ตัวอย่างการแยกตัวประกอบ

จงแก้สมการต่อไปนี้

x4-2x3-13x2+14x+24=0

วิธีทำ

p(x) คือ x4-2x3-13x2+14x และ a0= 24

(1. เลือก c ที่ทำให้ p(c) เท่ากับ 0 นั่นคือ)

p(2) = 16 - 16 - 52 + 28 +24 = 0

นั่นคือ จะได้ (x-2) เป็นตัวประกอบของ p(x)

(2. นำ (x-c) ไปหาร p(x) จะได้ผลหารเป็น q(x))

p(x) / (x-2) = x3-13x -12

q(x) มีดีกรีมากกว่า 2(ให้ทำซ้ำข้อ 1 โดยหาค่าc ที่ทำให้ q(c) =0)

เพราะฉะนั้น q(-1) = -1 +13 -12 =0
จะได้ว่า (x+1) เป็นตัวประกอบของ q(x)

(ทำซ้ำข้อ 2 อีกครั้งนะครับ)

q(x) / (x+1) = x2-x -12

(ในขั้นตอนนี้ ดีกรีของผลหารสุดท้ายเท่ากับ 2 จึงทำการแยกตัวประกอบได้เลยนะครับ)

จะได้ x2-x -12 = (x-4)(x+3)

ดังนั้น เราจะได้ว่า p(x) = (x-2)(x+1)(x-4)(x+3) = 0

เพราะฉะนั้น คำตอบของสมการนี้คือ x = 2, -1, 4, -3

ค่าสัมบูรณ์ของจำนวนจริง a ใดๆ เขียนแทนด้วย |a| หมายถึง ระยะทางจากจุด 0 จนถึงจุด บนเส้นจำนวน ตัวอย่างเช่น

เนื่องจากระยะทางต้องมีค่าเป็นจำนวนจริงบวกหรือศูนย์ ดังนั้น บทนิยามของค่าสัมบูรณ์สามารถเขียนได้ดังนี้

บทนิยาม

สำหรับจำนวนจริง x ทุกตัว ค่าสัมบูรณ์ของ x มีความหมายดังนี้

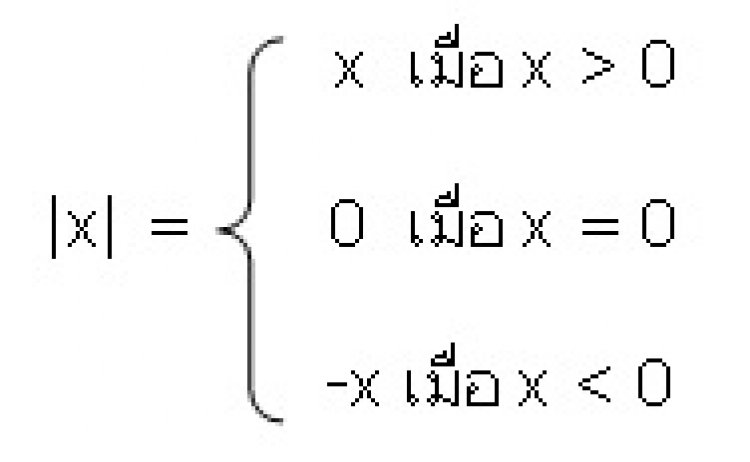
ทฤษฎีบทเกี่ยวกับค่าสัมบูรณ์

1. |x| = a ก็ต่อเมื่อ x = a หรือ x = -a

2. |x| = |-x|

3. |x| = |y| ก็ต่อเมื่อ x = y หรือ x = -y

4. |x| =√x2

5. |x|≥ 0

6. |x|≥ x

7. |xy| = |x| |y|

8. |x/y| = |x|/|y|

9. |x - y| = |y - x|

10. |x2| = |x|2= x2

11. |x + y| = |x| + |y| ก็ต่อเมื่อ xy≥ 0

12. |x|≤a ก็ต่อเมื่อ -a≤ x≤ a

13. |x|≥ a ก็ต่อเมื่อ x≤ -a หรือ x≥ a

14. |x + y|≤ |x| + |y|

15. |x - y|≥ |x| - |y|

การแก้สมาการที่มีค่าสัมบูรณ์

การแก้สมการที่มีค่าสัมบูรณ์ ต้องกำจัดค่าสัมบูรณ์ออกไปก่อน ซึ่งสามารถทำได้โดยใช้นิยามหรือ ทฤษฎีบทของค่าสัมบูรณ์ ดังที่ได้กล่าวไปแล้ว ทั้งนี้รูปแบบการกำจัดค่าสัมบูรณ์มีดังนี้

รูปแบบที่1ให้ p(x) เป็นพหุนามโดยที่ |p(x)| = a

เราสามารถเขียนสมการใหม่ได้เป็น p(x) = a หรือ p(x) = -a

ตัวอย่างจงหาเซตคำตอบของสมการ |x - 4| = 5

วิธีทำเราจะเขียนสมการใหม่ได้เป็น x – 4 = 5 หรือ x – 4 = -7

เพราะฉะนั้นเราจะได้ x = 9 หรือ x = -3

ดังนั้น เซตคำตอบคือ {-3, 9}

รูปแบบที่2ให้ p(x) และ q(x) เป็นพหุนามโดยที่ |p(x)| = |q(x)|

เราสามารถเขียนสมการใหม่ได้เป็น p(x) = q(x) หรือ p(x) = - q(x)

ตัวอย่างจงหาเซตคำตอบของสมการ |x - 2| = |3x - 4|

วิธีทำเราจะเขียนสมการใหม่ได้เป็น x - 2 = 3x - 4 หรือ x - 2 = -(3x - 4)

เพราะฉะนั้นเราจะได้ x = 1 หรือ x = 3/2

ดังนั้น เซตคำตอบคือ {1, 3/2}

รูปแบบที่3ให้ p(x) และ q(x) เป็นพหุนามโดยที่ |p(x)| = |q(x)|

เราสามารถเขียนสมการใหม่ได้เป็น p(x) = q(x) หรือ p(x) = - q(x) และ q(x) ≥ 0

ตัวอย่างจงหาเซตคำตอบของสมการ |2x - 5| = x - 1

วิธีทำเราจะเขียนสมการใหม่ได้เป็น 2x - 5 = x - 1 และ x - 1 ≥ 0

เพราะฉะนั้นเราจะได้ x = 4 และ x ≥ 1

หรือ 2x - 5 = -(x - 1) และ x - 1 ≥ 0

เพราะฉะนั้นเราจะได้ x = 2 และ x ≥ 1

ดังนั้น เซตคำตอบคือ {2, 4}

รูปแบบที่4ให้ p(x) เป็นพหุนามโดยที่ |p(x)| =- p(x)

เราสามารถเขียนสมการใหม่ได้เป็น p(x) ≤ 0

ตัวอย่างจงหาเซตคำตอบของสมการ |4x - 8| = 8 - 4x

วิธีทำเราจะเขียนสมการใหม่ได้เป็น 4x - 8 ≤ 0

เพราะฉะนั้นเราจะได้ 4x ≤ 8

x ≤ 8/4

เพราะฉะนั้นเราจะได้ x ≤ 2

ดังนั้น เซตคำตอบคือ {x | x ≤ 2}

รูปแบบที่5ให้ p(x) เป็นพหุนามโดยที่ |p(x)| = p(x)

เราสามารถเขียนสมการใหม่ได้เป็น p(x) ≥ 0

ตัวอย่างจงหาเซตคำตอบของสมการ |3x - 9| = 9 - 3x

วิธีทำเราจะเขียนสมการใหม่ได้เป็น 3x - 9 ≥ 0

เพราะฉะนั้นเราจะได้ 3x ≥ 9

x ≥ 9/3

เพราะฉะนั้นเราจะได้ x ≥ 3

ดังนั้น เซตคำตอบคือ {x | x ≥ 3}

รูปแบบที่6ให้ p(x) และ q(x) เป็นพหุนามโดยที่ |p(x) + q(x)| = |p(x)| + |q(x)|

เราสามารถเขียนสมการใหม่ได้เป็น p(x) q(x) ≥ 0