สถิติ (Statistics)
- 1. การแนะนำ
- 2. ทำไมเราต้องเรียนสถิติ?
- 3. การนำเสนอข้อมูลด้วยตารางแจกแจงความถี่
- 4. การนำเสนอข้อมูล (Representing data)
- 5. ฮิสโตแกรม และแผนภาพต้น-ใบ
- 6. ค่ากลาง (Central Value)
- 7. การหาตำแหน่งสัมพัทธ์ของข้อมูล
- 8. การกระจายของข้อมูล
- 9. ค่ามาตรฐาน และการแจกแจงปกติ
- 10. คุณสมบัติที่สำคัญของค่าเฉลี่ยเลขคณิต
- 11. ลักษณะการใช้ค่ากลาง
- 12. ทฤษฎีบางประการเกี่ยวกับค่าเฉลี่ยเลขคณิตและส่วนเบี่ยงเบนมาตรฐาน
- 13. สัมประสิทธิ์ความผันแปร (Coefficient of variation ; C.V)
- 14. การแจกแจงของตัวอย่าง
- 15. การแจกแจงความน่าจะเป็นของตัวแปรสุ่ม
- 16. ค่าเฉลี่ยเลขคณิต และ ความแปรปรวน กรณีสุ่มตัวอย่างออกมาพร้อมกัน
- - ทุกหน้า -
6 - การแจกแจงค่าสถิติ
การแจกแจงค่าสถิติ![]()
ประชากรมีการแจกแจงปกติ มี ค่าเฉลี่ยประชากร ?
และ ความแปรปรวนประชากร = ?2
สุ่มตัวอย่างขนาด n ได้ X1 ,X2 ,… , Xn



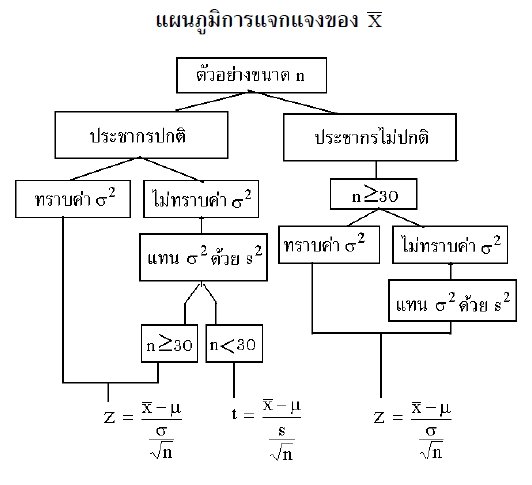

กลับไปที่เนื้อหา
หลังจากที่เราสอบเสร็จ ครูเชื่อว่าพวกเราก็คงใจจดจ่ออยากรู้ว่าตัวเองได้คะแนนเท่าไหร่ ผ่านค่าเฉลี่ย (ผ่านมีน, mean) หรือไม่ ใครได้ top ใครสอบตกไม่ตกบ้าง การที่คุณครูประจำวิชาจะให้เกรดได้นั้น กล่าวได้ว่าเป็นการวิเคราะห์ข้อมูลคะแนนการสอบของนักเรียน ก่อนจะตัดสินใจว่าใครควรได้เกรดเท่าไหร่
การวิเคราะห์ข้อมูลถือเป็นเรื่องสำคัญ เพราะจะนำไปใช้ต่อเพื่อการวางแผนหรือลงมือบางสิ่งบางอย่างต่อไป ในยุคนี้ปฏิเสธไม่ได้แล้วล่ะค่ะว่าชีวิตเราไม่เกี่ยวข้องกับข้อมูล มองไปทางไหนก็มีแต่ตัวเลข ดังนั้นมารู้จักกับศาสตร์ของสถิติกันหน่อยดีกว่า ^_^
การวิเคราะห์ข้อมูลอาจแบ่งเป็น 2 อย่าง ได้แก่
1) การวิเคราะห์เบื้องต้น เช่น การนำข้อมูลมาทำตารางแจกแจงความถี่ หาค่ากลางหรือค่าเฉลี่ย หาลักษณะการกระจาย เป็นต้น
2) การวิเคราะห์ขั้นสูง เช่น การประมาณแนวโน้มของข้อมูล การหาความสัมพันธ์ระหว่างข้อมูลมากกว่าหนึ่งชุด เป็นต้น
แต่จะทำการวิเคราะห์ข้อมูลได้ จะต้องมีข้อมูลในมือเสียก่อนนะคะ คำถามต่อมาคือ
จะเก็บรวบรวมข้อมูลอย่างไร?
เราสามารถแบ่งข้อมูลตามแหล่งที่มาได้เป็น 2 แบบ
1) ข้อมูลปฐมภูมิ (Primary Data) คือข้อมูลที่ได้จากการสำรวจเองโดยตรง เช่น ไปยืนนับจำนวนผู้ที่เดินผ่านหน้าประตูโรงเรียนตั้งแต่เวลา 7.00-8.00 น. การแจกแบบสอบถาม การทดลอง เป็นต้น
2) ข้อมูลทุติยภูมิ (Secondary Data) คือ การนำข้อมูลที่มีผู้สำรวจและวิเคราะห์ไว้แล้วมาใช้ เช่น ข้อมูลจากรายงาน จากหนังสือ จากหน่วยงานต่างๆ เป็นต้น
เมื่อเก็บข้อมูลมาได้แล้ว ข้อมูลอาจอยู่ในลักษณะในลักษณะหนึ่งใน 2 แบบนี้
1) ข้อมูลเชิงปริมาณ (Quantitative Data) เราสามารถใช้ตัวเลขในการแทนข้อมูลแบบนี้ได้ เช่น คะแนนสอบ น้ำหนัก ส่วนสูง อายุ ตัวเลขที่ใช้แทนก็อาจจะต่อเนื่องคือเป็นทศนิยมได้ (เช่น น้ำหนัก 50 kg, 50.1 kg, …) หรือตัวเลขไม่ต่อเนื่อง ไม่เป็นทศนิยมก็ได้ (เช่น ขายพัดลมเดือนนี้ได้ 1,000 ตัว เดือนก่อนขายได้ 950 ตัว เป็นต้น)
2) ข้อมูลเชิงคุณภาพ (Qualitative Data) เป็นข้อมูลที่ไม่เกี่ยวกับตัวเลขเลย เช่น ขนมที่ชอบ เพศ ศาสนา ซึ่งถ้าจะเอาไปวิเคราะห์อาจจะต้องใช้การกำหนดตัวเลขเพื่อแทนข้อมูลเหล่านี้
เมื่อข้อมูลดิบผ่านการวิเคราะห์แล้ว จะได้เป็น สารสนเทศ (information) ที่นำไปใช้ประโยชน์ต่อได้
กลับไปที่เนื้อหา
เราสามารถออกแบบการนำเสนอข้อมูลได้มากมายหลายแบบ ที่นิยมมากอันหนึ่งคือการใช้ตาราง (Table) ซึ่งจะทำให้เห็นภาพชัดเจนมากกว่าการอธิบายด้วยข้อความ
ตารางแจกแจงความถี่ (Frequency Distribution Table)คือ การนำเสนอข้อมูลที่ถูกจัดแบ่งออกเป็นกลุ่มๆ โดยให้ข้อมูลที่มีค่าใกล้เคียงกันอยู่ด้วยกัน
สมมติเรามีข้อมูลอายุของประชากรในหมู่บ้านหนึ่งจำนวน 30 คน ดังนี้
1 30 22 9 20 55 81 62 74 96
2555 413 5 12 14 1 31 46
2837 49 64 52 41 80 6 45 77
ขั้นตอนการทำตารางแจกแจงความถี่ มีดังนี้นะคะ
1) แบ่งค่าข้อมูลออกเป็นช่วงตามต้องการ เรียกว่า อันตรภาคชั้น (Class Interval) เช่น 1-10, 11-20, 20-30 เป็นต้น แต่ละอันตรภาคชั้นอาจแบ่งเท่ากันหรือไม่ก็ได้ หรืออาจเป็นช่วงเปิด (> 50, <20) ก็ได้
2) นับจำนวนข้อมูลที่ตกอยู่ในชั้นนั้น เรียกว่า ความถี่ (Frequency) แล้วใส่ลงไปในช่วงอันตรภาคที่ถูกต้อง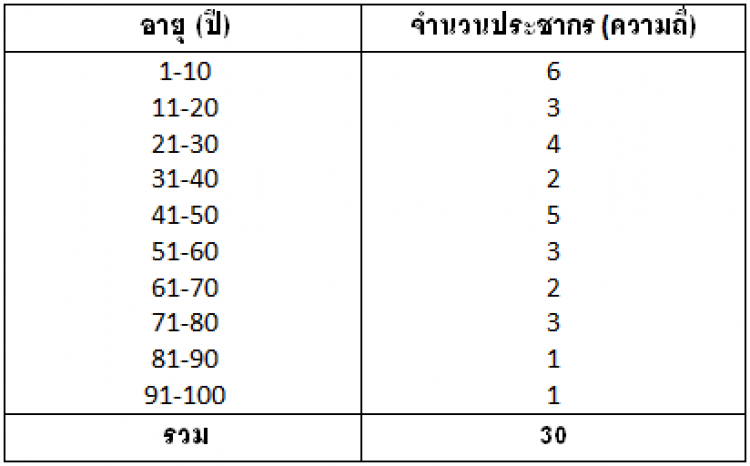
ค่าขอบบนและขอบล่างของแต่ละชั้น หาได้จากค่ากึ่งกลางระหว่างรอยต่อ ดังนั้นสำหรับชั้นที่สอง กล่าวได้ว่า 20.5 เป็นค่าขอบบน ในทำนองเดียวกัน 10.5 ก็จะเป็นค่าขอบล่าง
สำหรับความกว้างของอันตรภาคชั้นในตัวอย่างนี้เท่ากันหมด คือ 10
(ความกว้าง = ค่าขอบบน-ค่าขอบล่าง, 20.5-10.5 = 10)ถ้าอันตรภาคชั้นละเอียดไป เราก็สามารถแบ่งช่วงใหม่ได้ตามความเหมะสม เช่น 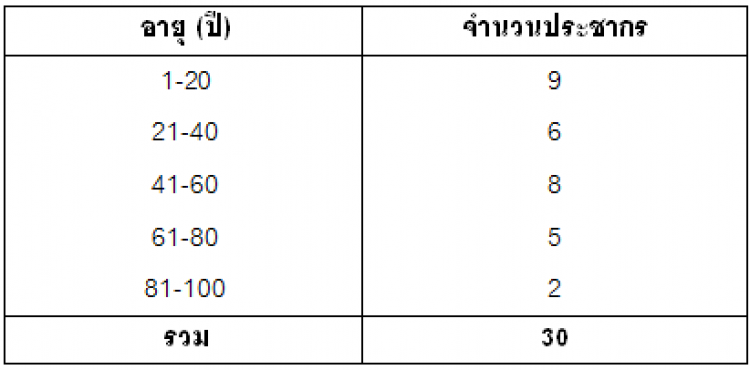 3) หากต้องการหาความถี่สะสม (Cumulative Frequency; ?f) สามารถทำได้โดยการนับจำนวนข้อมูลชั้นนั้น รวมกับจำนวนข้อมูลในชั้นที่ต่ำกว่าทั้งหมด
3) หากต้องการหาความถี่สะสม (Cumulative Frequency; ?f) สามารถทำได้โดยการนับจำนวนข้อมูลชั้นนั้น รวมกับจำนวนข้อมูลในชั้นที่ต่ำกว่าทั้งหมด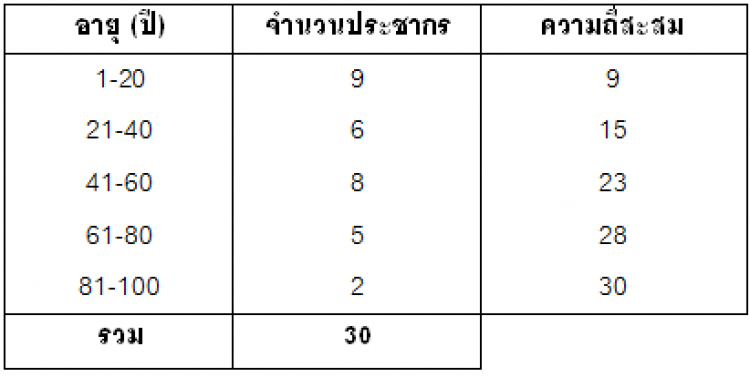 4) หากต้องการหาความถี่สัมพัทธ์ (Relative Frequency)หรือ ความถี่สะสมสัมพัทธ์ (Relative Cumulative Frequency) จะทำได้โดยการเปรียบเทียบความถี่หรือ ความถี่สะสมในชั้นนั้นกับความถี่รวม (ถ้าต้องการปรับหน่วยเป็นร้อยละก็คูณด้วย 100) ซึ่งผลรวมสุดท้ายของความถี่สัมพัทธ์จะเท่ากับ 1
4) หากต้องการหาความถี่สัมพัทธ์ (Relative Frequency)หรือ ความถี่สะสมสัมพัทธ์ (Relative Cumulative Frequency) จะทำได้โดยการเปรียบเทียบความถี่หรือ ความถี่สะสมในชั้นนั้นกับความถี่รวม (ถ้าต้องการปรับหน่วยเป็นร้อยละก็คูณด้วย 100) ซึ่งผลรวมสุดท้ายของความถี่สัมพัทธ์จะเท่ากับ 1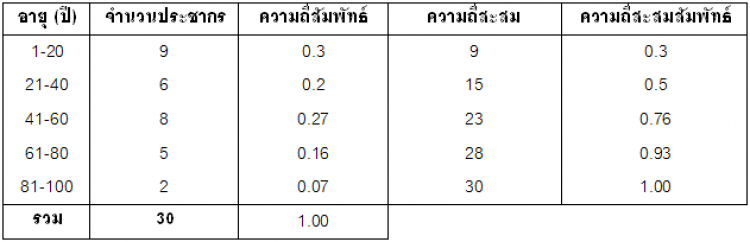
กลับไปที่เนื้อหา
เพื่อแสดงข้อมูลให้ดูง่ายและสามารถหาผลสรุปในลักษณะเปรียบเทียบ เราอาจใช้กราฟหรือแผนภูมิรูปแบบต่างๆ มาใช้ในการนำเสนอข้อมูล เช่น แผนภูมิแท่ง แผนภูมิรูปภาพ แผนภูมิวงกลมกราฟเส้นเป็นต้น
แผนภูมิแท่ง (Bar Chart)จะใช้เมื่อต้องการเปรียบเทียบข้อมูลที่มากกว่า 1 ค่า ความสูงของแต่ละแท่งกราฟแทนความถี่ (frequency) ของข้อมูล ซึ่งอาจเป็นจำนวนของข้อมูลดิบหรือเป็นตัวเลขสัดส่วนก็ได้ ปกติจะเขียนกำกับแกนไว้ด้วยว่าแสดงข้อมูลอะไรอยู่
ตัวอย่างแผนภูมิแท่ง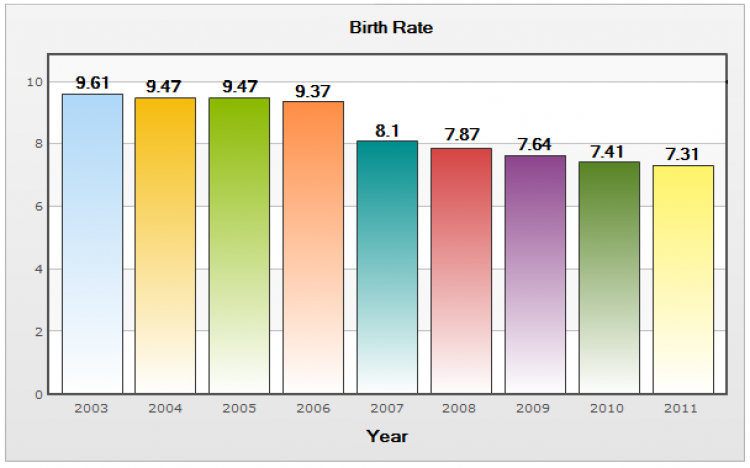
ที่มา: http://www.indexmundi.com/japan/birth_rate.html
แผนภูมิแท่งนี้แสดงอัตราการเกิดต่อประชากร 1000 คน ของประเทศญี่ปุ่น ระหว่างปี 2003-2011
แกนตั้ง (y) เป็นตัวเลขอัตราการเกิด ส่วนแกนนอน (x) เป็นปีที่ทำการบันทึก
จากแผนภูมิแท่งข้างต้น ลองตอบคำถามต่อไปนี้
1) ปีที่มีอัตราการเกิดสูงสุดและต่ำสุด คือปีใดบ้าง
2) แนวโน้มอัตราการเกิดของประชากรในประเทศญี่ปุ่นเป็นอย่างไร
ตอบก่อนจะดูเฉลยนะคะ
เฉลย
1) ปีที่อัตราเกิดสูงสุดและต่ำสุดคือปี 2003 และ 2011 ตามลำดับ
2) มีแนวโน้มลดลง
แผนภูมิรูปภาพ (Pictogram)จะใช้รูปภาพแทนข้อมูล ควรมีการกำหนดด้วยว่ารูปภาพนั้นแทนข้อมูลจำนวนเท่าใด
ตัวอย่างแผนภูมิรูปภาพ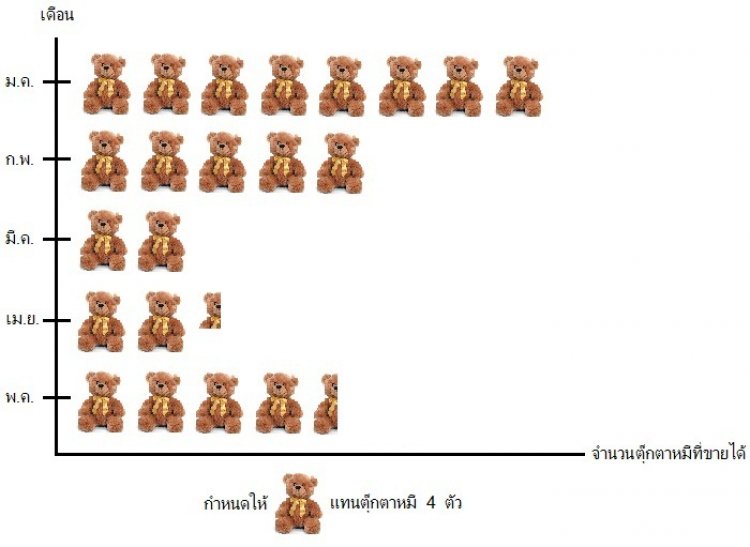
แผนภูมิรูปภาพนี้แสดงจำนวนตุ๊กตาหมีที่ร้าน Give Gifts ขายได้ตั้งแต่เดือนม.ค.-พ.ค. 2554
จากแผนภูมิข้างต้น ให้ตอบคำถามต่อไปนี้
1) เดือนใดมียอดขายตุ๊กตาหมีได้มากที่สุด และขายได้กี่ตัว
2) เดือนที่ขายได้น้อยที่สุด มียอดขายแตกต่างจากเดือนที่ขายได้มากที่สุดกี่ตัว
3) ยอดขายตุ๊กตาหมีรวมทั้ง 5 เดือน เป็นจำนวนกี่ตัว และถ้าตุ๊กตาหมีราคาตัวละ 299 บ. จะคิดเป็นยอดขายทั้งสิ้นกี่บาท
เฉลย
1) เดือนม.ค.ขายได้มากที่สุด จำนวน 32 ตัว
2) แตกต่างกัน 24 ตัว
3) ทั้งหมดขายไป 87 ตัว คิดเป็นยอดขายรวม 26,013 บาท
แผนภูมิวงกลม (Pie Chart / Circle Graph)จะแสดงจำนวนข้อมูลด้วยขนาดที่แตกต่างกันของส่วนของวงกลม มองในรูป % เมื่อเทียบกับพื้นที่วงกลมทั้งหมด
ตัวอย่างแผนภูมิวงกลม
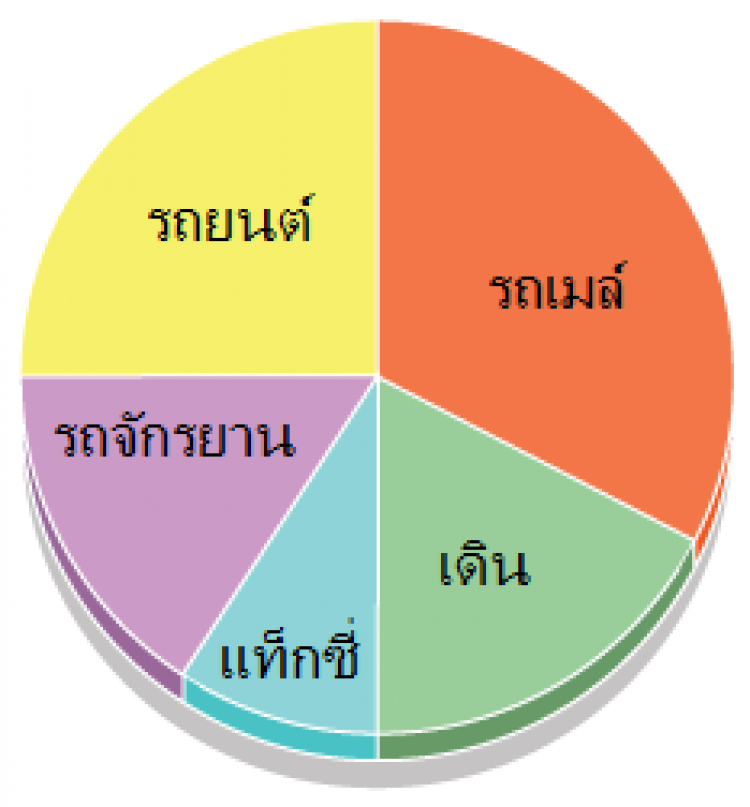
แผนภูมิวงกลมนี้แสดงผลการสำรวจวิธีการเดินทางมาโรงเรียนของนักเรียนชั้นม.6 โรงเรียนแห่งหนึ่งในจ.ปทุมธานี
ลองตอบคำถามต่อไปนี้ค่ะ
1) วิธีการเดินทางแบบใดเป็นที่นิยมที่สุด
2) นักเรียนที่เดินทางมาโดยรถยนต์ คิดเป็นสัดส่วนเท่าใดของนักเรียนทั้งหมด
3) ถ้านักเรียน 8 คนใช้วิธีเดินทางมาโดยรถยนต์ อยากทราบจำนวนนักเรียนทั้งหมดที่ร่วมตอบแบบสำรวจนี้
คำถามคงไม่ยากเกินไปใช่ไหมคะ ทำเสร็จแล้วลองตรวจคำตอบได้เลยค่ะ
เฉลย
1) เดินทางมาโดยรถเมล์
2) ? หรือ 25%
3) 32 คน
กราฟเส้น (Line Graph) มักถูกใช้เพื่อแสดงแนวโน้มข้อมูลในช่วงระยะเวลาที่ต่อเนื่อง เช่น หลายๆวัน หรือหลายๆชั่วโมง กราฟชนิดนี้จะพล็อตข้อมูลเป็นจุด และเชื่อมทุกจุดเข้าด้วยกันด้วยเส้นตรง ส่วนจุดเริ่มและจุดสุดท้ายในกราฟไม่ต้องลากต่อไปยังแกนข้อมูล
ตัวอย่างกราฟเส้น
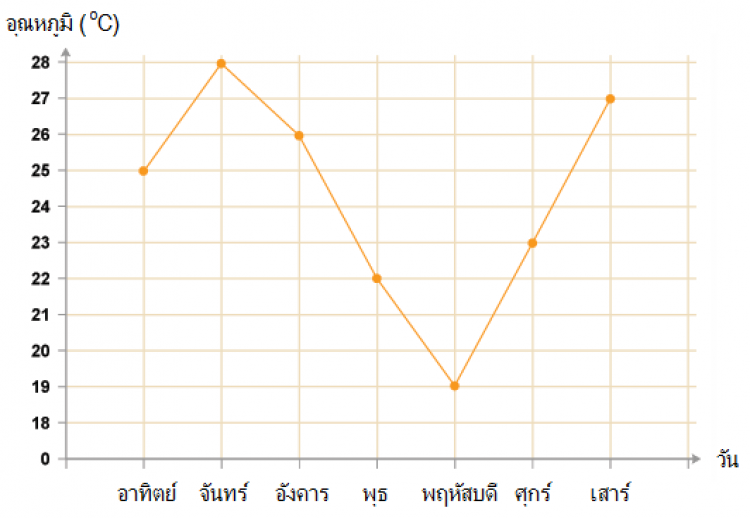
กราฟเส้นนี้แสดงอุณหภูมิของแต่ละวันในรอบหนึ่งสัปดาห์
เมื่อมองกราฟนี้จะเห็นได้ทันทีว่า วันจันทร์มีอุณหภูมิสูงที่สุด จากนั้นจะค่อยๆลดลงในตอนกลางของสัปดาห์และกลับมาสูงอีกครั้งในวันเสาร์
ลองตอบคำถามต่อไปนี้
1) วันไหนที่มีอุณหภูมิต่ำที่สุด และมีค่าเท่าใด
2) วันใดในสัปดาห์ที่มีอุณหภูมิ 26 องศาเซลเซียส
3) มีกี่วันที่มีอุณหภูมิต่ำกว่า 26 องศาเซลเซียส
เฉลย
1) วันพฤหัสบดี, 19 องศาเซลเซียส
2) วันอังคาร
3) 4 วัน
กลับไปที่เนื้อหา
ฮิสโตแกรม (Histogram) เป็นแผนภูมิแท่งที่บอกถึงความถี่ที่เกิดขึ้นในแต่ละอันตรภาคชั้น โดยแต่ละแท่งจะวางเรียงติดกัน แกนนอนจะกำกับด้วยค่าขอบบนและขอบล่างของชั้นนั้น หรือใช้ค่ากลาง (Midpoint) แกนตั้งเป็นค่าความถี่ในอันตรภาคชั้น ดังนั้นความสูงของแต่ละแท่งจะขึ้นอยู่กับความถี่นั่นเอง
ตารางแสดงความสูงของนักเรียนชั้นม.4 จำนวน 50 คน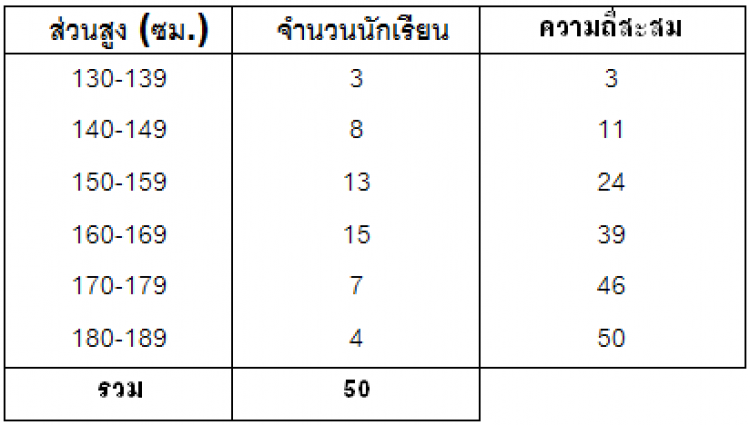
จากตารางนี้ สามารถสร้างฮิสโตแกรมแสดงความสูงของนักเรียน ได้ดังนี้
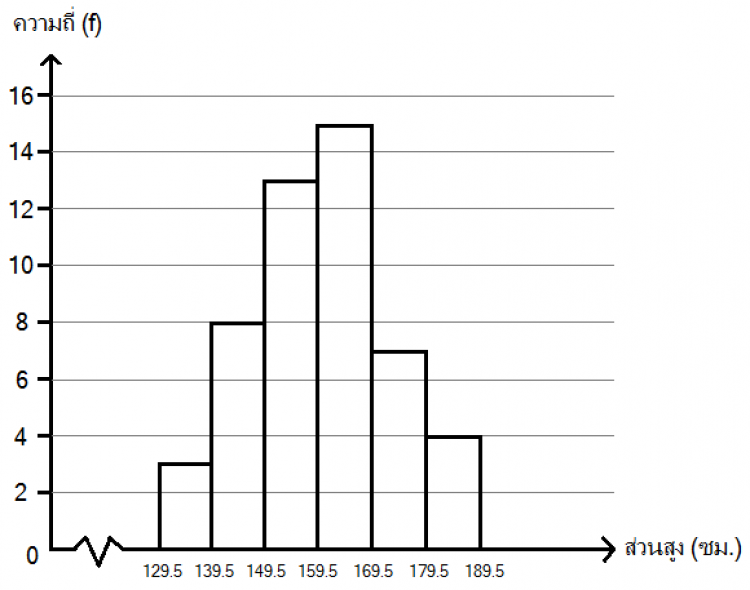
จากฮิสโตแกรมข้างต้น หากเราต้องการจะทำความเข้าใจรูปแบบของการกระจายของข้อมูล เราจะสร้างกราฟอีกอันเรียกว่ารูปหลายเหลี่ยมของความถี่ (Frequency Polygon) โดยการใช้เส้นตรงลากเชื่อมจุดกึ่งกลางของแต่ละแท่งในฮิสโตแกรมรูปบน โดยจุดเริ่มต้นและจุดปลายจะสมมติให้จบลงที่อันตรภาคชั้นก่อนและหลังอีกฟากละ 1 ชั้น จะได้รูปปิดดังกราฟต่อไปนี้
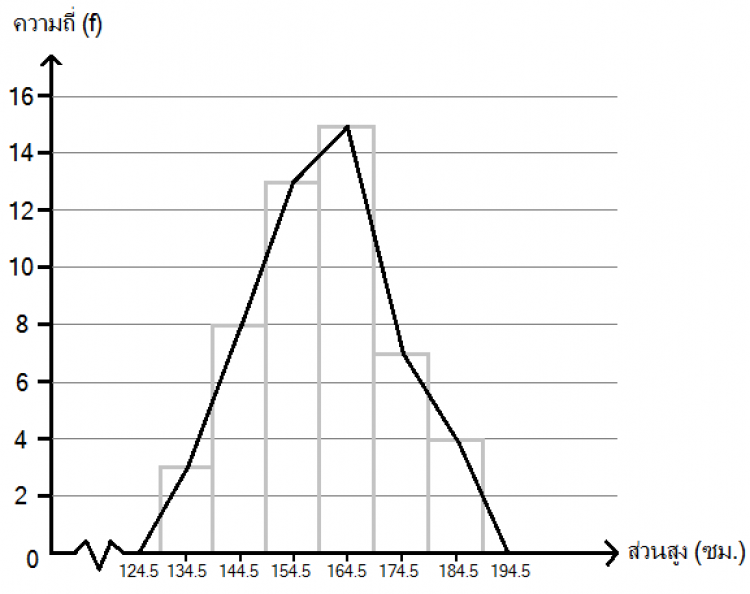
จากนั้นเราจะสร้างเส้นโค้งของความถี่ (Frequency Curve) โดยการปรับให้กราฟเป็นเส้นโค้งเรียบและให้พื้นที่ในรูปปิดใหม่ใกล้เคียงกับกราฟเดิม
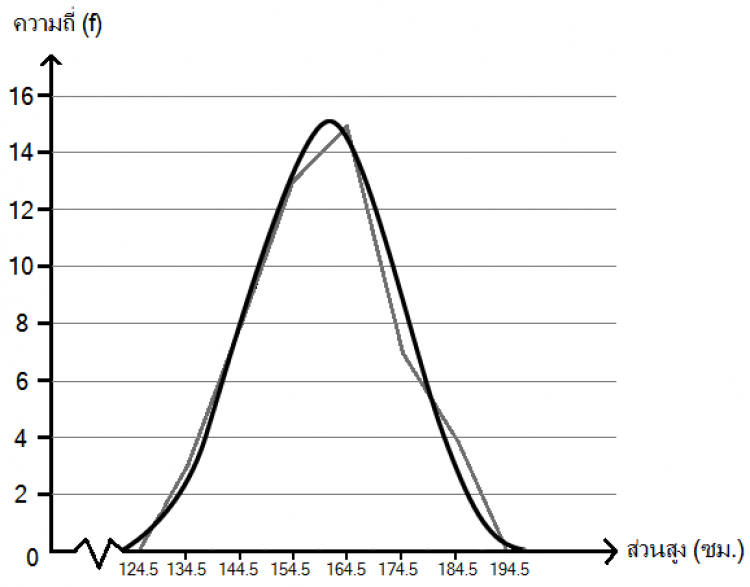
แผนภาพต้น-ใบ (Stem-and-Leaf Diagram) ใช้เพื่อจัดข้อมูลเป็นกลุ่มๆ และข้อมูลทุกตัวจะถูกแสดงในแผนภาพ ไม่เพียงแค่นับรวมว่าเป็นความถี่ในอันตรภาคชั้นเดียวกันเหมือนกับฮิสโตแกรม สมมติเรามีข้อมูลส่วนสูง(ซม.)ของนักเรียนชั้นป.6 จำนวน 20 คน ดังนี้
150 131 166 136 136134144 145 149140
145158 157 160 160 143 161 163 147 139
จะสามารถนำมาทำแผนภาพต้น-ใบ ได้ดังนี้
1. เลือกเอาตัวเลขหลักที่ซ้ำมาทำเป็น “ต้น” ในตัวอย่างนี้จะได้สองหลักซ้ายมือ
2. นำเลขที่เหลือ ของข้อมูลแต่ละตัว มาเขียนลงไปในช่อง “ใบ” (เช่น 150 ก็แยก 15 เป็น “ต้น” และ 0 เป็น “ใบ”)
3. ควรเรียงลำดับจากน้อยไปมาก เพื่อให้สะดวกต่อการวิเคราะห์
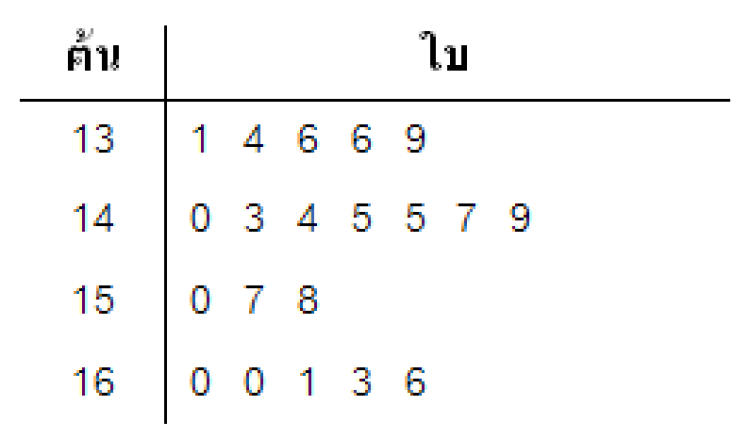
จากแผนภาพต้น-ใบนี้ จะบอกได้คร่าวๆว่าข้อมูลที่มีค่าต่ำที่สุดคือ 131 และสูงสุดคือ 166 ช่วงที่มีความถี่สูงสุดคือ 140 – 149
สมมติเราต้องการจะเปรียบเทียบชุดข้อมูล 2 กลุ่ม ก็สามารถทำ ได้ ตัวอย่างเช่น
ความสูงของนักเรียนห้องป.6/1 และ ป.6/2 เป็นดังนี้
ป. 6/1
150 131 166 136 136134144 145 149140
145158 157 160 160 143 161 163 147 139
ป. 6/2
162 163 163 172 157156154 165 161172
160148 144 160 175 190 169 155 157 176
เขียนเป็นแผนภาพต้น-ใบได้ดังนี้
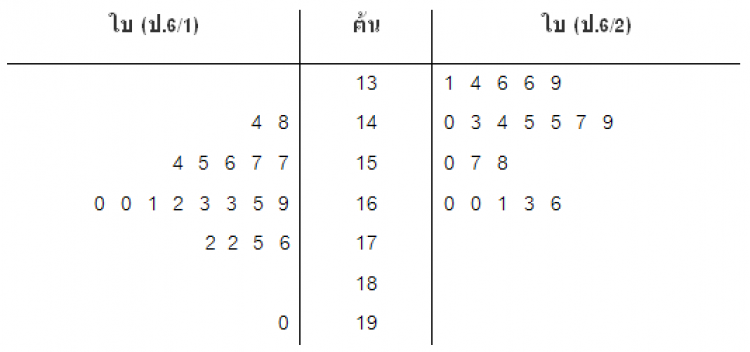
ซึ่งเราจะสามารถวิเคราะห์ข้อมูลทั้ง 2 กลุ่มอย่างคร่าวๆ ได้ว่า
1) นักเรียนชั้นป.6/1 ส่วนใหญ่มีความสูงอยู่ในช่วง 150-159 ซม. ในขณะที่นักเรียนชั้นป.6/2 ส่วนใหญ่มีความสูงอยู่ระหว่าง 140-149 ซม.
2) นักเรียนคนที่เตี้ยที่สุดอยู่ชั้นป.6/2 สูง 131 ซม.ส่วนนักเรียนที่สูงที่สุดอยู่ชั้นป.6/1 สูง 190 ซม.
3) ชั้นป.6/1 มีนักเรียนที่สูงผิดปกติ 1 คน
4) ความสูงเฉลี่ยชั้นป.6/1 น่าจะมากกว่าชั้นป.6/2
กลับไปที่เนื้อหา
ค่าของข้อมูลที่รวบรวมมาได้อาจมีความหลากหลายแตกต่างกันไป เพื่อให้สามารถทำการวิเคราะห์ข้อมูลอย่างกว้างๆได้ เราจะหาเลขจำนวนหนึ่งซึ่งใช้เป็นตัวแทนข้อมูลทั้งหมด เรียกตัวเลขนี้ว่า ค่ากลาง ซึ่งค่ากลางที่นิยมใช้มี 3 แบบ ได้แก่ ค่าเฉลี่ยเลขคณิต(Mean) มัธยฐาน(Median) และฐานนิยม(Mode)
I. ค่าเฉลี่ยเลขคณิต (Mean)
เป็นค่ากลางที่คำนวณจากทุกๆค่าข้อมูล ดังนั้นจึงเหมาะกับชุดข้อมูลที่มีค่าใกล้เคียงกัน ไม่มีค่าโดดสูงหรือต่ำกว่าปกติ
การหาค่าเฉลี่ยเลขคณิตทำได้ดังนี้
1) สำหรับข้อมูลที่ยังไม่ได้แจกแจงความถี่;
เมื่อ xi คือข้อมูลตัวที่ i, i=1, 2, .., N และ N เป็นจำนวนข้อมูลทั้งหมด
2) สำหรับข้อมูลที่แจกแจงความถี่แล้ว;
เมื่อ xi เป็นกึ่งกลางชั้นที่ i, fi คือความถี่ชั้นที่ i, i=1, 2, .., k, k เป็นจำนวนชั้นทั้งหมด และN เป็นจำนวนข้อมูลทั้งหมด
II. มัธยฐาน (Median)
เมื่อเรียงข้อมูลจากน้อยไปมากหรือมากไปน้อยแล้ว ค่าที่อยู่ตรงกึ่งกลางจะเรียกว่ามัธยฐาน ค่านี้ทำให้เราทราบว่ามีจำนวนข้อมูลที่มากกว่าหรือน้อยกว่าค่ากลางนี้อยู่เป็นจำนวนเท่าๆกัน ดังนั้นมัธยฐานจึงยังใช้ได้ดีแม้ว่าจะมีบางค่าข้อมูลที่ต่ำหรือสูงผิดปกติปะปนอยู่ในกลุ่มข้อมูลนั้น
1) สำหรับข้อมูลที่ยังไม่ได้แจกแจงความถี่ (เรียงลำดับแล้ว); Med = ค่าข้อมูลที่ตำแหน่ง
เมื่อ N เป็นจำนวนข้อมูลทั้งหมด
2) สำหรับข้อมูลที่แจกแจงความถี่แล้ว;Med
เมื่อ L เป็นค่าขอบล่างของชั้นที่มีค่ามัธยฐานอยู่ (ตำแหน่งของค่ามัธยฐานหาได้จาก N/2),
W เป็นค่าความกว้างของอันตรภาคชั้นนั้น,
เป็นความถี่สะสมตั้งแต่ชั้นแรกจนถึงชั้นที่ m (ชั้นที่ต่ำกว่าขอบล่าง) และ
fMed เป็นความถี่ของอันตรภาคชั้นนั้น
III. ฐานนิยม (Mode)
ฐานนิยม คือค่าที่ปรากฏซ้ำมากที่สุดในชุดข้อมูล เป็นค่าที่ให้ความสำคัญกับความถี่ของข้อมูล เช่น การลงคะแนนเลือกตั้งประธานนักเรียน เบอร์ที่มีความถี่มากที่สุดถือเป็นค่าฐานนิยม
1) สำหรับข้อมูลที่ยังไม่ได้แจกแจงความถี่; Mo = ข้อมูลที่ปรากฏซ้ำมากที่สุด
2) สำหรับข้อมูลที่แจกแจงความถี่แล้ว; Mo
เมื่อ L เป็นค่าขอบล่างของชั้นที่มีค่าฐานนิยมอยู่ (ชั้นที่ความถี่สูงสุด),
W เป็นค่าความกว้างของอันตรภาค (ทุกๆชั้นมีความกว้างเท่ากัน),
dL เป็นค่าผลต่างของความถี่ของชั้นนั้นกับความถี่ของชั้นถัดลงมา(ต่ำกว่า 1 ชั้น) และ
dU เป็นค่าผลต่างของความถี่ของชั้นนั้นกับความถี่ของชั้นถัดขึ้นไป(สูงกว่า 1 ชั้น)
ข้อสังเกตุ: จากค่ากลางทั้ง 3 แบบ ค่ามัธยฐาน(Median) จะมีค่าอยู่ระหว่างค่าเฉลี่ยเลขคณิต(Mean) และฐานนิยม (Mode) เสมอ แต่่ค่าเฉลี่ยเลขคณิตอาจสูงหรือต่ำกว่าค่าฐานนิยมได้ แล้วแต่ลักษณะของการกระจายของข้อมูล
..........................................................................................................
=> ตัวอย่างการหาค่ากลางทั้ง 3 แบบ สำหรับข้อมูลที่ยังไม่ได้แจกแจงความถี่ <=
ข้อมูลรายได้ต่อเดือนของชาวบ้าน 10 คนในหมู่บ้านแห่งหนึ่ง เป็นดังนี้
5500 3100 4700 6300 3100 2800 4500 6100 5000 5200
จงหาค่าเฉลี่ยเลขคณิต มัธยฐาน และฐานนิยมของข้อมูลชุดนี้
1) ค่าเฉลี่ยเลขคณิต หาจาก บาท
2) มัธยฐาน เอาข้อมูลมาเรียงลำดับก่อนจะได้
2800 3100 3100 4500 4700 5000 5200 5500 6100 6300
ตำแหน่งของมัธยฐาน = (10+1)/2 = 5.5 นั่นคือเป็นตำแหน่งตรงกลางระหว่างตำแหน่งที่ 5 กับ 6 ดังนั้นต้องคิดเฉลี่ยแบ่งครึ่งเอา
ค่ามัธยฐาน = (4700+5000)/2 = 4850 บาท
3) ฐานนิยม คือ ตัวเลขที่ปรากฏซ้ำกันบ่อยที่สุด ซึ่งก็คือ 3100 บาท
..........................................................................................................
=> ตัวอย่างการหาค่ากลางทั้ง 3 แบบ สำหรับข้อมูลที่แจกแจงความถี่แล้ว <=
จากตารางแสดงความสูงของนักเรียนชั้นม.4 จำนวน 50 คน ข้างล่างนี้
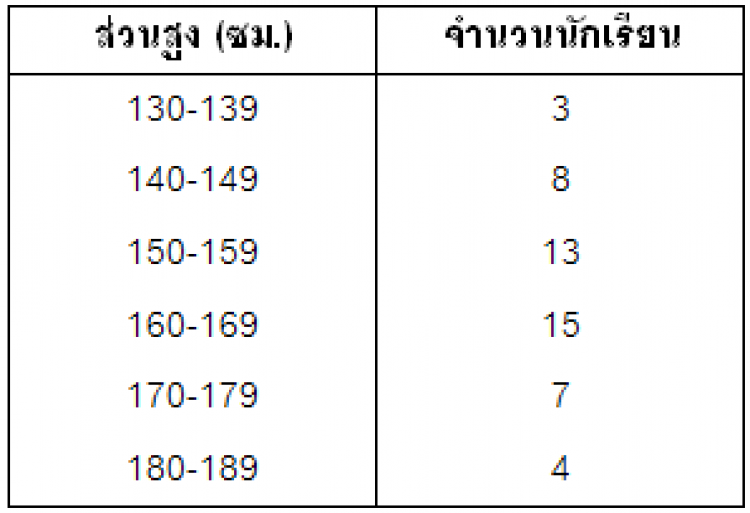
จงหาค่าเฉลี่ยเลขคณิต มัธยฐาน และฐานนิยม
1) ค่าเฉลี่ยเลขคณิต, ต้องหาจุดกึ่งกลางของแต่ละอันตรภาคชั้นก่อน
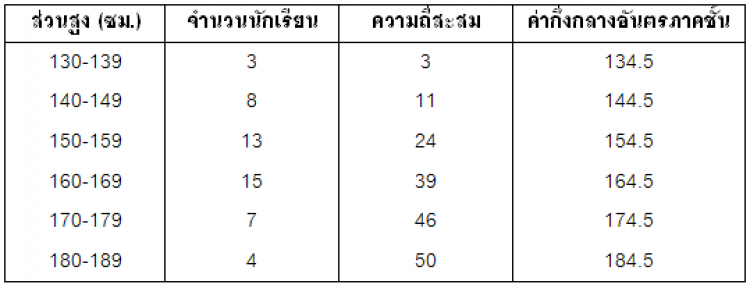
ซม.
2) มัธยฐาน, ต้องหาความถี่สะสมก่อน
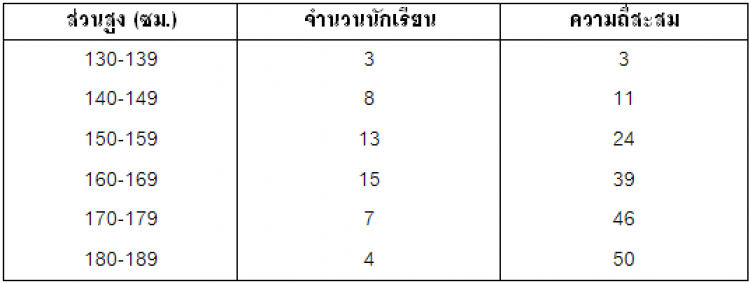
ตำแหน่งของมัธยฐาน = N/2 = 50/2 = 25 จากนั้นไปดูความถี่สะสมว่าลำดับของนักเรียนคนที่ 25 ควรอยู่ที่ชั้นใด
จะพบว่ามัธยฐานตกอยู่ในอันตรภาคชั้น 160-169
ซม.
3) ฐานนิยม
ตำแหน่งของฐานนิยมจะอยู่ในอันตรภาคชั้นที่มีความถี่สูงสุด ในตัวอย่างนี้คือ 160-169
ซม.
กลับไปที่เนื้อหา
จากหัวข้อก่อนเรื่องค่ากลางของข้อมูล มัธยฐานเป็นค่าที่สามารถหาได้จากการพิจารณาตำแหน่งที่อยู่ตรงกลางของชุดข้อมูลเมื่อเรียงลำดับแล้ว ซึ่งค่ามัธยฐานบอกให้เราทราบว่ามีข้อมูลที่น้อยกว่าหรือมากกว่าค่ากลางนี้เป็นปริมาณเท่าๆ กัน
นอกจากการหาตำแหน่งข้อมูลที่อยู่ตรงกลางแล้ว เรายังสามารถหาตำแหน่งข้อมูลตัวใดก็ได้ ตรงไหนก็ได้ในชุดข้อมูลนั้นโดยเรียงลำดับข้อมูลจากน้อยไปมากก่อน จากนั้นแบ่งข้อมูลออกเป็นกลุ่มๆ และเทียบตำแหน่งข้อมูลตัวที่ต้องการกับข้อมูลที่เหลือ ซึ่งเราเรียกว่า การหาตำแหน่งสัมพัทธ์ของข้อมูล
ตำแหน่งสัมพัทธ์ของข้อมูลที่นิยมใช้มีอยู่ 3 แบบ ได้แก่
1) ควอร์ไทล์ (Quartile) - ภายหลังจากเรียงข้อมูลแบบน้อยไปมากแล้ว จะแบ่งข้อมูลออกเป็น 4 กลุ่มเท่าๆ กัน ซึ่งจะเกิดจุดแบ่ง 3 จุด ดูรูปประกอบนะคะ
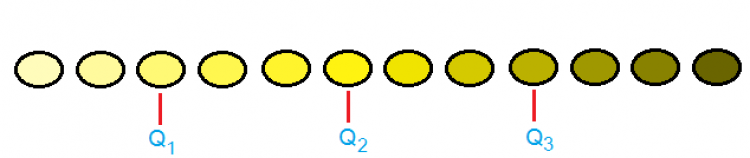
เรียกจุดแบ่งเหล่านี้ว่า ควอร์ไทล์ที่ 1 (Q1), ควอร์ไทล์ที่ 2 (Q2) และ ควอร์ไทล์ที่ 3 (Q3) ตามลำดับ
- ที่ Q1 บอกให้เราทราบว่า มีจำนวนข้อมูลที่มีค่าน้อยกว่าจุดนี้อยู่ประมาณ 1/4 (25%) และมีจำนวนข้อมูลที่มีค่ามากกว่าจุดนี้อยู่ประมาณ 3/4 (75%)
- ที่ Q2 เราทราบได้ว่า มีจำนวนข้อมูลที่มีค่าน้อยกว่าจุดนี้อยู่ประมาณครึ่งหนึ่งของข้อมูลทั้งหมด (50%) และมีจำนวนข้อมูลที่มีค่ามากกว่าจุดนี้อยู่ประมาณครึ่งหนึ่งเช่นกัน
- ที่ Q3 ทำให้เราทราบว่า มีจำนวนข้อมูลที่มีค่าน้อยกว่าจุดนี้อยู่ประมาณ 3/4 (75%) และมีจำนวนข้อมูลที่มีค่ามากกว่าจุดนี้อยู่ประมาณ 1/4 (25%)
โดยเราจะสามารถหาตำแหน่งควอร์ไทล์ได้ดังนี้
สำหรับข้อมูลที่ยังไม่ได้แจกแจงความถี่ ปปป ปปปQr = ข้อมูล ณ ตำแหน่งที่
สำหรับข้อมูลที่แจกแจงความถี่แล้ว ปปปปปปปปปQr =
เมื่อ L เป็นค่าขอบล่างของชั้นที่มีค่า Qr อยู่,
W เป็นค่าความกว้างของอันตรภาคชั้นนั้น,
เป็นความถี่สะสมตั้งแต่ชั้นแรกจนถึงชั้นที่ m (ชั้นที่ต่ำกว่าขอบล่าง) และ
fQr เป็นความถี่ของอันตรภาคชั้นนั้น
อย่าลืมว่า ข้อมูลจะต้องเรียงลำดับจากน้อยไปมากก่อนเสมอ
2) เดไซล์ (Decile) – แนวคิดเดียวกับแบบแรก แต่เดไซส์นั้นจะแบ่งข้อมูลออกเป็น 10 กลุ่ม และเราจะเรียกจุดแบ่งทั้ง 9 จุดนี้ว่า เดไซล์ที่ 1 (D1), เดไซล์ที่ 2 (D2), เดไซล์ที่ 3 (D3), … , ไปจนถึง ควอร์ไทล์ที่ 9 (D9) ตามลำดับ
ตำแหน่งของเดไซล์แต่ละจุด หาได้จาก
สำหรับข้อมูลที่ยังไม่ได้แจกแจงความถี่ ปปปปปปDr = ข้อมูล ณ ตำแหน่งที่
สำหรับข้อมูลที่แจกแจงความถี่แล้ว ปปปปปปปปDr =
เมื่อ L เป็นค่าขอบล่างของชั้นที่มีค่า Dr อยู่,
W เป็นค่าความกว้างของอันตรภาคชั้นนั้น,
เป็นความถี่สะสมตั้งแต่ชั้นแรกจนถึงชั้นที่ m (ชั้นที่ต่ำกว่าขอบล่าง) และ
fDr เป็นความถี่ของอันตรภาคชั้นนั้น
3) เปอร์เซนไทล์ (Percentile) - เป็นการแบ่งข้อมูลที่เรียงลำดับแล้วออกเป็น 100 กลุ่ม หรือพูดง่ายๆ ว่า มีข้อมูลอยู่กี่ % ที่มีค่ามากกว่า(หรือน้อยกว่า) ข้อมูลที่สนใจนั่นเอง ตัวอย่างที่นิยมใช้เปอร์เซนไทล์ก็เช่น การพิจารณาจัดตำแหน่งของนักเรียนคนที่สนใจ โดยนำผลการเรียนของนักเรียนคนนั้นมาเทียบกับเพื่อนร่วมชั้น เป็นต้น
จะหาตำแหน่งเปอร์เซนไทล์ได้ดังนี้
สำหรับข้อมูลที่ยังไม่ได้แจกแจงความถี่ ปปปปปป Pr = ข้อมูล ณ ตำแหน่งที่
สำหรับข้อมูลที่แจกแจงความถี่แล้ว ปปปปปปปปปPr =
เมื่อ L เป็นค่าขอบล่างของชั้นที่มีค่า Pr อยู่,
W เป็นค่าความกว้างของอันตรภาคชั้นนั้น,
เป็นความถี่สะสมตั้งแต่ชั้นแรกจนถึงชั้นที่ m (ชั้นที่ต่ำกว่าขอบล่าง) และ
fPr เป็นความถี่ของอันตรภาคชั้นนั้น
------------------------------------------------------------------------------------------
ตัวอย่างการหาค่าตำแหน่งสัมพัทธ์ สำหรับข้อมูลที่ยังไม่ได้แจกแจงความถี่
ข้อมูลรายได้ต่อเดือนของชาวบ้าน 10 คนในหมู่บ้านแห่งหนึ่ง เป็นดังนี้
5500 3100 4700 6300 3100 2800 4500 6100 5000 5200
ให้หาค่ามัธยฐาน ควอร์ไทล์ที่ 3 และเปอร์เซนไทล์ที่ 60 ของข้อมูลชุดนี้
Soln ก่อนอื่นต้องเรียงลำดับข้อมูลจากน้อยไปมากก่อน จะได้
2800 3100 3100 4500 4700 5000 5200 5500 6100 6300
1) มัธยฐาน
ตำแหน่งของมัธยฐาน = (10+1)/2 = 5.5 ซึ่งเป็นตำแหน่งตรงกลางระหว่างตำแหน่งที่ 5 กับ 6 ดังนั้นต้องคิดเฉลี่ยแบ่งครึ่งเอา
ค่ามัธยฐาน = (4700+5000)/2 = 4850 บาท
2) ควอร์ไทล์ที่ 3
ตำแหน่ง Q3 = 8.25 ซึ่งอยู่ระหว่างตำแหน่งที่ 8 และ 9 (5500 และ 6100)
Q3 = 5500+0.25(6100-5500) = 5650 บาท
3) เปอร์เซนไทล์ที่ 60
ตำแหน่ง P60 = 6.6 ซึ่งอยู่ระหว่างตำแหน่งที่ 6 และ 7 (5000 และ 5200)
P60 = 5000+0.6(5200-5000) = 5120 บาท
------------------------------------------------------------------------------------------
ตัวอย่างการหาค่าตำแหน่งสัมพัทธ์ สำหรับข้อมูลที่แจกแจงความถี่แล้ว
จากตารางแสดงความสูงของนักเรียนชั้นม.4 จำนวน 50 คน ข้างล่างนี้
|
ส่วนสูง (ซม.) |
จำนวนนักเรียน |
|
130-139 |
3 |
1) นิดและหน่อยเป็นนักเรียนในกลุ่มนี้ ถ้าความสูงของนิดอยู่ที่เปอร์เซนไทล์ที่ 20 ส่วนความสูงของหน่อยอยู่ที่ควอร์ไทล์ที่ 3 ถามว่าใครสูงกว่าใคร และสูงกว่ากี่เซนติเมตร
Soln ก่อนจะหาตำแหน่งสัมพัทธ์ จะต้องหาความถี่สะสมก่อน ได้เป็นตารางนี้
|
ส่วนสูง (ซม.) |
จำนวนนักเรียน |
ความถี่สะสม |
|
130-139 |
3 |
3 |
คำนวณหาความสูงของนิด
ตำแหน่ง P20 = 10 ซึ่งอยู่ในอันตรภาคชั้น 140-149
P20 = ซม.
คำนวณหาความสูงของหน่อย
ตำแหน่ง Q3 = 37.5 ซึ่งอยู่ในอันตรภาคชั้น 160-169
Q3 = ซม.
เพราะฉะนั้นจะได้ว่า หน่อยสูงกว่านิด และสูงกว่าอยู่ 168.5-145.86 = 22.64 ซม.
2) ความสูง 169.5 คิดเป็นเดไซล์ที่เท่าใด
ความสูง 169.5 เป็นขอบบนของอันตรภาคชั้น 160-169 พอดี
นั่นหมายความว่า มีคนต่ำว่านี้ 39 คน และสูงกว่านี้ 11 คน
ดังนั้นจึงคิดเป็นเดไซล์ที่
กลับไปที่เนื้อหา
ในบางครั้ง ค่ากลางไม่สามารถบอกคุณลักษณะโดยรวมที่แท้จริงของชุดข้อมูลได้ ตัวอย่างเช่น ข้อมูลรายได้ต่อเดือนของชาวบ้าน 20 คนจาก 2 ตำบล เป็นดังนี้
รายได้ชาวบ้านตำบลที่ 1: 5500 3100 4700 6300 3100 2800 4500 6100 5000 5200
รายได้ชาวบ้านตำบลที่ 2: 500 2300 500 2300 1100 800 1500 13100 14000 10200
ซึ่งทั้งสองตำบลชาวบ้านมีรายได้เฉลี่ยเท่ากับ 4630 บาท แต่รายได้ของชาวบ้านตำบลที่ 2 ค่อนข้างมีความแตกต่างกันมากกว่าในตำบลที่ 1
เพื่อให้สามารถอธิบายลักษณะของกลุ่มข้อมูลได้ดีขึ้น เราจะอาศัยค่าอีกค่าหนึ่ง เรียกว่า ค่าการกระจายของข้อมูล ซึ่งถ้าค่ายิ่งมากจะบอกว่าข้อมูลมีการกระจัดกระจายมาก ค่าการกระจายที่นิยมใช้มี 4 แบบ ได้แก่
1) พิสัย (Range) – เป็นการวัดความแตกต่างของช่วงค่าแบบหยาบๆ วัดได้ง่าย แต่จะผิดพลาดได้หากข้อมูลในกลุ่มมีค่าต่ำเกินไปหรือสูงเกินไป
สำหรับข้อมูลที่ยังไม่ได้แจกแจงความถี่:xxxxxxR= xmax-xmin
เมื่อ xmax และ xmin เป็นค่าข้อมูลที่มากที่สุดและน้อยที่สุดตามลำดับ
สำหรับข้อมูลที่แจกแจงความถี่แล้ว:xxxxxxxxxR= Umax-Lmin
เมื่อ Umax และ Lmin เป็นค่าขอบบนของชั้นที่มีข้อมูลตัวที่มากที่สุด และค่าขอบล่างของชั้นที่มีข้อมูลตัวที่น้อยที่สุด ตามลำดับ
2) ส่วนเบี่ยงเบนควอร์ไทล์ (Quartile Deviation) - จะคำนวณโดยใช้ข้อมูลควอร์ไทล์ที่ 1 และ 3เท่านั้น สามารถใช้ได้กับชุดข้อมูลที่มีข้อมูลบางตัวสูงหรือต่ำมากๆ และยังใช้ได้กับการแจกแจงความถี่ที่มีชั้นเปิด
วิธีการคำนวณจะใช้แบบเดียวกัน ทั้งข้อมูลที่ยังไม่ได้แจกแจง และแบบแจกแจงความถี่แล้ว
เมื่อ Q3 และ Q1 คือข้อมูลที่ควอร์ไทล์ที่ 3 และ 1 ตามลำดับ
3) ส่วนเบี่ยงเบนเฉลี่ย (Mean/Average Deviation) - การคำนวณจะยุ่งยากขึ้น แต่เป็นการวัดการกระจายที่ละเอียดกว่าสองแบบก่อนหน้านี้
สำหรับข้อมูลที่ยังไม่ได้แจกแจงความถี่:xxxxxxxx
เมื่อxi คือข้อมูลตัวที่ i, คือค่าเฉลี่ยเลขคณิต, N คือจำนวนข้อมูลทั้งหมด
สำหรับข้อมูลที่แจกแจงความถี่แล้ว:xxxxxxxxxxx
เมื่อ fi เป็นความถี่ชั้นที่ i, xi เป็นกึ่งกลางชั้นที่ i, คือค่าเฉลี่ยเลขคณิต, N คือจำนวนข้อมูลทั้งหมด
4) ส่วนเบี่ยงเบนมาตรฐาน (Standard Deviation) - เป็นค่าที่นิยมใช้ที่สุด เนื่องจากละเอียดและน่าเชื่อถือ นำไปวิเคราะห์ข้อมูลในขั้นสูงได้
สำหรับข้อมูลที่ยังไม่ได้แจกแจงความถี่:xxxxxxxx
เมื่อxi คือข้อมูลตัวที่ i,คือค่าเฉลี่ยเลขคณิต, N คือจำนวนข้อมูลทั้งหมด
สูตรหลังสุดจะเป็นที่นิยมเนื่องจากสะดวกต่อการคำนวณ
สำหรับข้อมูลที่แจกแจงความถี่แล้ว:xxxxxxxxxxx
เมื่อ fi เป็นความถี่ชั้นที่ i, xi เป็นกึ่งกลางชั้นที่ i, คือค่าเฉลี่ยเลขคณิต, N คือจำนวนข้อมูลทั้งหมด
-------------------------------------------------------------------------------------------------
ตัวอย่างการคำนวณค่าการกระจายของข้อมูล
จงหาพิสัย, ส่วนเบี่ยงเบนควอร์ไทล์, ส่วนเบี่ยงเบนเฉลี่ย และส่วนเบี่ยงเบนมาตรฐานของข้อมูลรายได้ชาวบ้านแต่ละตำบล
รายได้ชาวบ้านตำบลที่ 1: 5500 3100 4700 6300 3100 2800 4500 6100 5000 5200
รายได้ชาวบ้านตำบลที่ 2: 500 2300 500 2300 1100 800 1500 13100 14000 10200
Soln
เรียงลำดับข้อมูลทั้งสองชุด จากน้อยไปมากเป็นอันดับแรก
รายได้ชาวบ้านตำบลที่ 1:2800 31003100 4500 4700 5000 520055006100 6300
รายได้ชาวบ้านตำบลที่ 2: 500 500 800 1100 1500 2300 2300 10200 13100 14000
1) พิสัย
R1= 6300 - 2800 = 3500
R2 = 14000 - 500 = 13500
ดังนั้น พิสัยของรายได้ชาวบ้านตำบลที่ 1 และ 2 เท่ากับ 3500 บ.และ 13500 บ. ตามลำดับ Ans
2) ส่วนเบี่ยงเบนควอร์ไทล์
จะต้องหา Q3 และ Q1 ของแต่ละชุดข้อมูลให้ได้ก่อน
ตำบลที่ 1, QD1:
Q3 อยู่ในตำแหน่ง
Q1 อยู่ในตำแหน่ง
ตำบลที่ 2, QD2:
Q3 อยู่ในตำแหน่ง 8.25ดังนั้น
Q1 อยู่ในตำแหน่ง 2.75 ดังนั้น
ส่วนเบี่ยงเบนควอร์ไทล์ของรายได้ชาวบ้านตำบลที่ 1 และ 2 มีค่าเป็น 1275 และ 5100 ตามลำดับ
จะเห็นได้ว่าส่วนเบี่ยงเบนควอร์ไทล์ของตำบลที่ 2 มีค่าสูงกว่าของตำบลที่ 1 Ans
3) ส่วนเบี่ยงเบนเฉลี่ย
จะต้องหาค่า
ส่วนเบี่ยงเบนเฉลี่ยของรายได้ชาวบ้านตำบลที่ 1 และ 2 มีค่าเป็น 1004 และ 4682 ตามลำดับ Ans
4) ส่วนเบี่ยงเบนมาตรฐาน
ใช้ที่หาได้ในข้อ 3) มาใช้ในการคำนวณ ซึ่งการคิดก็จะคล้ายๆกัน เพียงแต่ผลต่างแต่ละตัวต้องยกกำลังสอง และเพิ่ม Square root เข้าไปด้วย
ส่วนเบี่ยงเบนมาตรฐานของรายได้ชาวบ้านตำบลที่ 1 และ 2 มีค่าเป็น 1192.52 และ 5219.78 ตามลำดับ Ans
กลับไปที่เนื้อหา
ค่ามาตรฐาน (Standard Score; z) เป็นค่าที่ใช้เปรียบเทียบข้อมูลระหว่างชุดได้ เนื่องจากได้ปรับค่าเฉลี่ยเลขคณิตและส่วนเบี่ยงเบนมาตรฐานให้เท่ากันแล้ว
เมื่อ xi เป็นข้อมูลชุดที่ i และ i = 1, 2, …, N
คุณสมบัติของค่ามาตรฐานที่ควรทราบ
1) ผลรวมของ z ของทุกข้อมูลมีค่าเป็นศูนย์
2) โดยทั่วไป ข้อมูลจำนวน 95% จะอยู่ในช่วง z = -2 ถึง z = 2 หรือกล่าวได้ว่าอยู่ในช่วง
3) พิสัยมีค่าประมาณ 4s
~ เส้นโค้งความถี่ ~
เส้นโค้งความถี่ใช้แสดงลักษณะการกระจายของข้อมูล มี 3 แบบได้แก่
1) เส้นโค้งปกติ (Normal curve/Bell-shaped curve)
2) เส้นโค้งเบ้ขวา (Positively Skewed Curve)
3) เส้นโค้งเบ้ซ้าย (Negatively Skewed Curve)
สังเกตว่าเส้นโค้งแต่ละแบบ จะบอกถึงตำแหน่งค่าเฉลี่ยที่แตกต่างกันด้วย
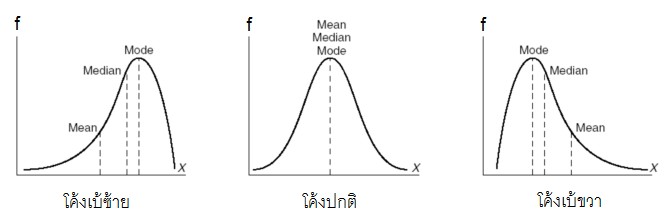
Tip: เพื่อไม่ให้สับสนกับการเบ้ของกราฟ สมัยที่คุณครูเป็นนักเรียน อาจารย์สอนว่าให้ “ดูหาง”ของกราฟ ถ้าหางด้านไหนยาวกว่าเรียกว่าเบ้ด้านนั้น เช่น กราฟเบ้ซ้ายจะมีหางด้านซ้ายยาวกว่าค่ะ ^_^
เนื่องจากการสร้างเส้นโค้งมาจากการสร้างฮิสโตแกรม ดังนั้นพื้นที่รวมใต้กราฟทั้งหมดจึงเท่ากับจำนวนข้อมูลหรือความถี่รวมพอดี (พื้นที่รวมมักถูกปรับให้เป็น 1 เพื่อให้นำไปคำนวณได้สะดวกค่ะ)
ปกติแล้วข้อมูลแต่ละชุดจะมีค่ากลางที่แตกต่างกัน เพื่อให้สามารถนำมาเปรียบเทียบการกระจายได้ ในแต่ละชุดข้อมูลเราจะปรับให้ค่า x เป็นค่า z ก่อน แล้วนำไปพล็อตเส้นโค้ง ซึ่งเส้นโค้งที่ได้จะเรียกว่าเส้นโค้งปกติ
คุณลักษณะของเส้นโค้งปกติ
1) พื้นที่รวมใต้เส้นโค้ง (ความถี่รวม) จะเท่ากับ 1
2) ในการใช้ตารางเพื่อหาพื้นที่ใต้เส้นโค้งนั้น ค่าพื้นที่ที่แสดงวัดระหว่าง z=0 ไปถึง z ใดๆ โดย z เป็นค่าบวกเท่านั้น(พื้นที่ด้านขวาของกราฟ) ดังนั้นเราจึงสามารถหาพื้นที่ด้านซ้ายที่เหลือได้โดยหลักความสมมาตร
3) หากค่า z หรือค่าพื้นที่ใต้โค้งที่ต้องการ ไม่พอดีกับค่าที่ให้มาในตาราง จะต้องเทียบสัดส่วนเพื่อให้ได้ค่าที่ต้องการ
4) การหาค่าเปอร์เซนไทล์ (หรือเดไซล์, ควอร์ไทล์) สามารถทำได้โดยการเอาพื้นที่ไปเทียบเป็นค่า z ใช้วิธีคิดว่าพื้นที่ทั้งหมดเป็น 1.00 (100 ส่วน) จากหางกราฟด้านซ้ายมาถึงกึ่งกลางเส้นโค้ง จะมีพื้นที่เท่ากับ 0.5 (50 ส่วน)
--------------------------------------------------------------------------------------------
ตัวอย่างการทำโจทย์
1) นักเรียนคนหนึ่งสอบวิชาคณิตศาสตร์และวิชาดนตรีได้ 48 และ 35 คะแนนตามลำดับ โดยค่าเฉลี่ยของวิชาคณิตศาสตร์เป็น 45 และของวิชาภาษาอังกฤษเป็น 32 คะแนน ส่วนเบี่ยงเบนมาตรฐานเป็น 12 กับ 10 ตามลำดับ นักเรียนคนนี้ทำคะแนนวิชาใดได้ดีกว่ากัน
Soln
หาค่ามาตรฐานแต่ละวิชา แล้วจึงนำมาเปรียบเทียบกัน
จากสูตร
จะเห็นว่า นักเรียนคนนี้ทำคะแนนวิชาดนตรีได้ดีกว่า Ans
--------------------------------------------------------------------------------------------
2) ตารางต่อไปนี้แสดงพื้นที่ใต้โค้งปกติมาตรฐาน ระหว่าง z = z ถึง z = -z
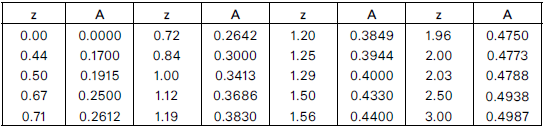
ให้หาพื้นที่โค้งปกติมาตรฐาน ในช่วงค่า z ต่อไปนี้
2.1) z = 2 ถึง 3
2.2) z = 0 ถึง -2.03
2.3) z < -1.19
Soln
2.1) พื้นที่ใต้กราฟ จะแสดงจากค่า z = 0 ไป +z (ไปด้านขวาของกราฟ)
พื้นที่ z = 0 ถึง 2 มีค่าเท่ากับ 0.4773
พื้นที่ z = 0 ถึง 3 มีค่าเท่ากับ 0.4987
เพราะฉะนั้น พื้นที่ระหว่าง z = 2 ไปถึง z=3 มีค่าเท่ากับ 0. 4987 - 0.4773 = 0.0214 Ans
2.2) สามารถใช้ตารางได้ โดยดูจากค่า z = 2.03 (กราฟสมมาตรกัน)
เพราะฉะนั้นพื้นที่ใต้กราฟ z = 0 ถึง -2.03 เท่ากับ 0.4788 Ans
2.3) z < -1.19
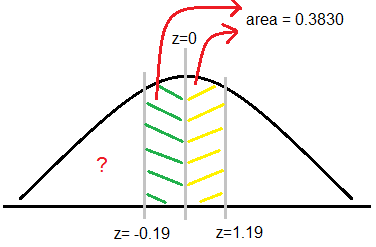
จากภาพ จะเห็นได้ว่า พื้นที่ใต้กราฟ z < -1.19 (ตรงเครื่องหมาย “?”) จะเท่ากับ 0.5 – 0.3830 = 0.117 Ans
--------------------------------------------------------------------------------------------
3) ถ้าคะแนนสอบวิชาชีววิทยามีการแจกแจงปกติ โดยมีคะแนนเฉลี่ยเท่ากับ 60 และความแปรปรวนเท่ากับ 25 ถ้าวิชานี้ต้องได้ตั้งแต่ 54 คะแนนขึ้นไปจึงจะสอบผ่าน นายเอ บี และซี ทราบว่าตนเองอยู่ตำแหน่งเปอร์เซนไทล์ที่ 10, 15 และ 33 ตามลำดับ
จงหาว่า นายซีสอบได้กี่คะแนน และใครสอบผ่านบ้าง
ให้ตารางพื้นที่ใต้กราฟมาดังนี้ 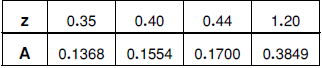
Soln
3.1) หาคะแนนสอบของนายซี
จากโจทย์
นายซีอยู่ที่เปอร์เซนไทล์ที่ 33, P33 จะได้ว่าอยู่ซีกซ้ายของกราฟ (ตรงกลางคือ P50) และมีพื้นที่ใต้กราฟเป็น 0.17 ซึ่งจากตารางข้างต้น จะได้ z = 0.44 ดังนั้น z ที่ถูกต้องจะเป็น -0.44 (ต้องเป็นค่าลบ เพราะอยู่ด้านซ้ายของกราฟ)
จากสูตร
คะแนนสอบของนายซี = 57.2 คะแนน Ans
3.2) ใครสอบผ่านบ้าง
ตอนนี้เราทราบแล้วว่านายซีสอบผ่าน ทีนี้จะมาหาคะแนนของนายเอ และบี ด้วยวิธีการเดียวกัน
P10 มีพื้นที่ใต้กราฟเท่ากับ 0.4 และ P15 มีพื้นที่ใต้กราฟเท่ากับ 0.35 แต่เมื่อดูในตารางแล้วปรากฏว่าไม่มีค่าพื้นที่ตรงตามที่ต้องการสำหรับ P10 ส่วน P15 มีพื้นที่ใกล้เคียงคือ 0.3849 ซึ่งอาจจะใช้วิธีเทียบกลับเพื่อหา z ได้ อย่างไรก็ตามจะเห็นว่ายังหา z ของ P10 ไม่ได้อยู่ดี
แต่โจทย์บอกว่า นักเรียนต้องสอบให้ได้คะแนนตั้งแต่ 54 ขึ้นไปจึงจะผ่าน ดังนั้นเราจะหาว่าคะแนนนี้คิดเป็นเปอร์เซนไทล์ที่เท่าใด และดูว่าถ้าคนไหนอยู่ในเปอร์เซนไทล์ที่สูงกว่านี้ ก็ถือว่าสอบผ่าน
เริ่มจากหาค่ามาตรฐานก่อน; ไปดูในตารางที่ z = 1.2 จะได้พื้นที่เป็น 0.3849
แต่ z = -1.2 อยู่ด้านซ้ายของกราฟ ดังนั้น (0.5-0.3849)x100 = 11.51
สรุปว่านักเรียนที่สอบผ่านต้องอยู่ตั้งแต่เปอร์เซนไทล์ที่ 11.51 เป็นต้นไป
แสดงว่า นักเรียนที่สอบผ่านมีเพียง 2 คน คือนายบีและซี Ans
กลับไปที่เนื้อหา
คุณสมบัติที่สำคัญของค่าเฉลี่ยเลขคณิต
(1) ค่าเฉลี่ยเลขคณิตเมื่อคูณกับจำนวนข้อมูลทั้งหมด จะได้ผลรวมของข้อมูลทุกๆค่า กล่าวคือ
![]()
(2) ผลรวมของความแตกต่างระหว่างแต่ละค่าของข้อมูลกับค่าเฉลี่ยเลขคณิตของข้อมูลนั้นจะเท่ากับ 0 เสมอ กล่าวคือ
![]()
(3) ผลรวมกำลังสองของความแตกต่างระหว่างแต่ละค่าของข้อมูลกับค่าเฉลี่ยเลขคณิตของข้อมูลชุดนั้นจะมีค่าน้อยที่สุด นั่นคือ
![]()
(4) ค่าเฉลี่ยเลขคณิตของข้อมูลใดๆ จะต้องอยู่ระหว่างค่าน้อยที่สุดกับค่าที่มากที่สุดของข้อมูลนั้น กล่าวคือ
![]()
เมื่อ X min คือ ค่าน้อยที่สุดในข้อมูล
X max คือ ค่ามากที่สุดในข้อมูล
(5) ถ้าชุดข้อมูล X สัมพันธ์กับชุดข้อมูล Y ในรูปฟังก์ชันเส้นตรง นั่นคือ ถ้า Yi = aXi + b, i = 1, 2, 3,…, N และ a, b เป็นค่าคงที่ แล้ว จะสัมพันธ์กับ ดังนี้
![]()
เมื่อ ![]() คือ ค่าเฉลี่ยเลขคณิตของข้อมูลชุด Y
คือ ค่าเฉลี่ยเลขคณิตของข้อมูลชุด Y
![]() คือ ค่าเฉลี่ยเลขคณิตของข้อมูลชุด X
คือ ค่าเฉลี่ยเลขคณิตของข้อมูลชุด X
ตัวอย่าง
ให้ X แทนราคาซื้อ และ Y แทนราคาขายสินค้าอย่างหนึ่ง ราคาขายกับราคาซื้อมีความสัมพันธ์เป็น ![]() ถ้าค่าเฉลี่ยของราคาซื้อเป็น 30 บาทอยากทราบว่าค่าเฉลี่ยของราคาขายเป็นเท่าใด
ถ้าค่าเฉลี่ยของราคาซื้อเป็น 30 บาทอยากทราบว่าค่าเฉลี่ยของราคาขายเป็นเท่าใด
วิธีทำ จากฟังก์ชันความสัมพันธ์ระหว่างราคาขายกับราคาซื้อเป็น
![]()
นั่นคือ ![]()
แต่ ![]()
![]()
= 44
แสดงว่าค่าเฉลี่ยของราคาขายสินค้าชนิดนี้เท่ากับ 44 บาท
กลับไปที่เนื้อหา
ลักษณะการใช้ค่ากลาง
ค่ากลางต่างๆ นิยมใช้ในลักษณะดังนี้
- ค่าเฉลี่ยเลขคณิต เป็นค่ากลางที่นิยมใช้มากที่สุด เพราะคำนวณง่ายมีความแปรผันระหว่างค่าเฉลี่ยเลขคณิตกับข้อมูลน้อยที่สุด เป็นค่ากลางที่เป็นสื่อต่อความเข้าใจง่าย และมีคุณสมบัติที่จะโยงไปสู่การอนุมานทางสถิติต่อไปได้ดี
- ค่าฐานนิยม เป็นค่ากลางที่ใช้วัดถึงความนิยมที่สะท้อนให้เห็นถึงแนวโน้มของส่วนรวม และเป็นค่ากลางค่าเดียวที่ใช้คำนวณกับข้อมูลเชิงคุณภาพได้
- ค่ามัธยฐาน เป็นค่ากลางที่ใช้กับข้อมูลเชิงปริมาณเพื่อต้องการทราบว่าค่ากึ่งกลางของข้อมูลจะอยู่ ณ ค่าใด มักจะหาค่ามัธยฐานกับข้อมูลที่ไม่สามารถวัดได้ด้วยค่าเฉลี่ยเลขคณิต เช่น ข้อมูลที่เป็นตารางแจกแจงความถี่แบบมีชั้นเปิด หรือข้อมูลที่มีลักษณะผิดปกติที่ใช้ค่าเฉลี่ยเลขคณิตอธิบายแล้วจะทำให้ผู้อ่านเข้าใจความหมายผิดไป เป็นต้น
ความสัมพันธ์ระหว่างค่าเฉลี่ยเลขคณิต ค่ามัธยฐาน และฐานนิยม
ในกรณีที่ข้อมูลมีค่าฐานนิยมเพียง 1 ค่าและการแจกแจงของข้อมูลค่อนข้างจะมีลักษณะสมมาตรคือ ไม่เบ้ไปทางซ้ายหรือขวามากนัก ค่าเฉลี่ยเลขคณิต ค่ามัธยฐาน และฐานนิยมจะมีความสัมพันธ์กันดังนี้
ค่าเฉลี่ยเลขคณิต – ค่าฐานนิยม = 3 (ค่าเฉลี่ยเลขคณิต – ค่าค่ามัธยฐาน)
ความสัมพันธ์ระหว่าง เปอร์เซนไทล์, เดไซล์, ควอไทล์ และค่ามัธยฐาน
- P50 = D5 = Q2 = มัธยฐาน
- P25 = Q1
- P75 = Q3
ตัวอย่าง
จากข้อมูลแสดงสอบวิชาคณิตศาสตร์ของนิสิต 7 คน ดังนี้ 55, 50, 59, 61, 65, 80, และ 71 จงหา P30, D5 และ Q3
วิธีทำ
หา P30 มีขั้นตอนดังนี้
1.หาตำแหน่ง P30
P30 มีตำแหน่งตรงกับข้อมูลค่าที่ ![]()
2.เรียงลำดับข้อมูลจากน้อยไปหามากได้
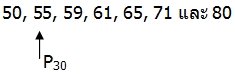
3. เทียบบัญญัติไตรยางศ์ ดังนี้
ตำแหน่งต่างกัน 1 ตำแหน่ง ค่าของข้อมูลต่างกัน = 59 – 55 = 4 คะแนน
ตำแหน่งต่างกัน 0.4 ตำแหน่ง ค่าของข้อมูลต่างกัน = 4 x 0.4 = 1.6 คะแนน
ฉะนั้น P30 = 55 + 1.6 = 56.6 คะแนน
หมายความว่า มีนิสิต 30 เปอร์เซ็นต์ที่สอบไล่ได้คะแนนน้อยกว่า หรือเท่ากับ 56.6 คะแนน ส่วนนิสิตอีก 70 เปอร์เซ็นต์จะสอบไล่ได้คะแนนสูงกว่า 56.6 คะแนน
หา D5
1.หาตำแหน่ง D5
D5 มีตำแหน่งตรงกับข้อมูลตัวที่ ![]()
2.เรียงลำดับข้อมูลจากน้อยไปหามากดังนี้
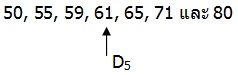
3.D5 คือ ค่าของข้อมูลตัวที่ 4 = 61
D5 = 61 คะแนน
หมายความว่า ถ้าแบ่งคะแนนสอบของนิสิต 7 คน ออกเป็น 10 ส่วนเท่าๆกันจะมีคะแนนของนิสิตอยู่ 5 ส่วนที่มีค่าน้อยกว่าหรือเท่ากับ 61 คะแนน และมีคะแนนของนิสิตอีก 5 ส่วนจะมีคะแนนสูงกว่า 61 คะแนน
หา Q3
1.หาตำแหน่ง Q3
Q3 มีตำแหน่งตรงกับข้อมูลค่าที่![]()
2.เรียงลำดับข้อมูลจากน้อยไปหามากดังนี้

3.ในที่นี้ค่า Q3 จะตรงกับค่าของข้อมูลตัวที่ 6 คือ 71
Q3 = 71 คะแนน
หมายความว่าถ้าแบ่งคะแนนของนิสิต 7 คนออกเป็น 4 ส่วนเท่าๆกัน จะมีคะแนนของนิสิตอยู่ 3 ส่วนมีค่าน้อยกว่าหรือเท่ากับ 71 คะแนน และมีคะแนนของนิสิตอีก 1 ส่วนจะมีค่ามากกว่า 71 คะแนน
กลับไปที่เนื้อหา
ทฤษฎีบางประการเกี่ยวกับค่าเฉลี่ยเลขคณิตและส่วนเบี่ยงเบนมาตรฐาน
ทฤษฎีที่ 1 ถ้าข้อมูลแต่ละตัวมีค่าลดลงหรือเพิ่มขึ้นเท่ากันทุกค่า สมมติให้เท่ากับค่า k ซึ่งเป็นค่าคงที่ แล้วค่าเฉลี่ยเลขคณิตใหม่จะมีค่าเพิ่มขึ้นหรือลดลงเท่ากับจำนวนค่าคงที่ k นั้น ส่วนค่าความแปรปรวนและค่าส่วนเบี่ยงเบนมาตรฐานจะมีค่าเท่าเดิมไม่เปลี่ยนแปลง
ทฤษฎีที่ 2 ถ้าข้อมูลแต่ละตัวมีค่าเพิ่มขึ้น k เท่าของค่าเดิม ตัวกลางเลขคณิตใหม่จะมีค่าเป็น k เท่าของค่าเดิม ส่วนเบี่ยงเบนมาตรฐานใหม่จะเป็น k เท่าของส่วนเบี่ยงเบนมาตรฐานเดิม และค่าความแปรปรวนใหม่จะมีค่าเป็น k2 เท่าของค่าเดิม
นั่นคือถ้าให้ ?, ? และ ?2 เป็นค่าเฉลี่ยเลขคณิต ส่วนเบี่ยงเบนมาตรฐาน และค่าความแปรปรวนตามลำดับ ของข้อมูลชุดหนึ่งประกอบด้วย x1, x2, x3, …, xN ให้ k = ค่าคงที่ ดังนี้
- ข้อมูล x1 k, x2 k, x3 k, …, xN k จะมีค่าเฉลี่ยเลขคณิตเท่ากับ ? k มีค่าส่วนเบี่ยงเบนมาตรฐานเท่ากับ ? และมีค่าความแปรปรวนเท่ากับ ?2
- ข้อมูล kx1, kx2, kx3, …, kxN จะมีค่าเฉลี่ยเลขคณิตเท่ากับ k? และมีค่าส่วนเบี่ยงเบนมาตรฐานเท่ากับ k? และมีค่าความแปรปรวนเท่ากับ k2?2
สมบัติที่สำคัญของส่วนเบี่ยงเบนมาตรฐาน
- ส่วนเบี่ยงเบนมาตรฐานมีค่าเป็นบวกเสมอ
- ถ้าคำนวณหาส่วนเบี่ยงเบนมาตรฐานโดยใช้ค่ากลางของมูลชนิดชนิดอื่นๆ ที่ไม่ใช่ค่าเฉลี่ยเลขคณิต ส่วนเบี่ยงเบนมาตรฐานที่จะได้จะมีค่ามากกว่าส่วนเบี่ยงเบนมาตรฐานที่ใช้ค่าเฉลี่ยเลขคณิตเสมอ นั่นคือ
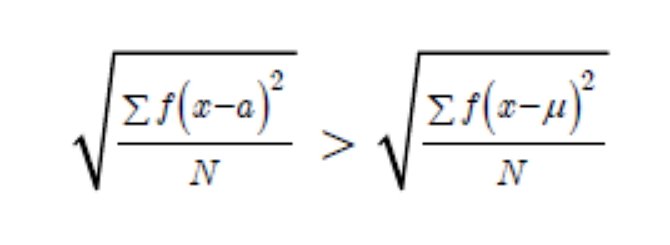
อสมการนี้เป็นจริงเสมอ เมื่อ a เป็นจำนวนจริงใดๆ ที่ไม่เท่ากับค่าเฉลี่ยเลขคณิต
ความแปรปรวนรวม (Combined Variances)
ถ้ามีข้อมูล k ชุดซึ่งมีขนาดข้อมูลเป็น N1, N2, N3, …, Nk ตามลำดับ โดยที่ค่าเฉลี่ยเลขคณิตของข้อมูลทุกชุดเท่ากันหมด และให้ ?12, ?22, ?32, …, ?k2, เป็นความแปรปรวนของข้อมูลชุดที่หนึ่ง ชุดที่ 2 ถึงชุดที่ k ตามลำดับ
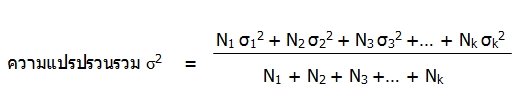
ถ้าค่าเฉลี่ยเลขคณิตของข้อมูลทุกชุดไม่เท่ากันหมด ความแปรปรวนรวมหาได้ดังนี้
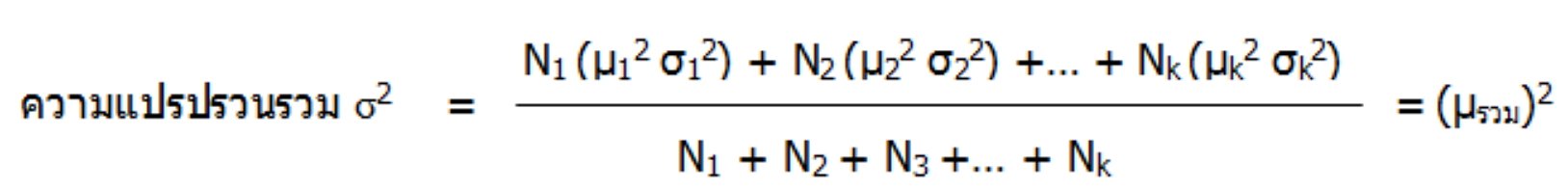
ตัวอย่าง
ความแปรปรวนของอายุสมาชิกครอบครัวหนึ่ง ซึ่งมี 4 คน เท่ากับ 9 (ปี)2 และความแปรปรวนของอายุสมาชิกอีกครอบครัวหนึ่งซึ่งมี 6 คน เท่ากับ 4 (ปี)2 ถ้าค่าเฉลี่ยเลขคณิตของสมาชิกทั้งสองครอบครัวเท่ากัน อยากทราบว่า อีก 2 ปีข้างหน้าความแปรปรวนรวมของอายุของสมาชิกทั้งสองครอบครัวเป็นเท่าใด
วิธีทำ
เนื่องจากค่าเฉลี่ยเลขคณิตของข้อมูลสองชุดเท่ากัน จะได้ความแปรปรวนของอายุของสมาชิกทั้งสองครอบครัวในปัจจุบัน คือ
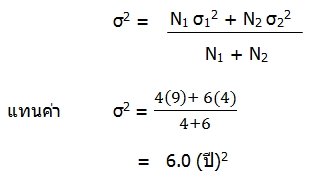
อีก 2 ปีข้างหน้าสมาชิกทุกคนของทั้งสองครอบครัวจะมีอายุเพิ่มขึ้นคนละ 2 ปี แต่การเพิ่มของอายุจะไม่มีผลกระทบต่อความแปรปรวน นั่นคือ ความแปรปรวนของอายุสมาชิกทั้งสองครอบครัวจะเท่าเดิม ดังนั้น ความแปรปรวนรวมจะยังมีค่าเท่าเดิมเช่นกัน กล่าวคืออีก 2 ปีข้างหน้าความแปรปรวนรวมของอายุของสมาชิกทั้งสองครอบครัว เท่ากับ 6.0 (ปี)2
กลับไปที่เนื้อหา
สัมประสิทธิ์ความผันแปร (Coefficient of variation ; C.V)
กรณีต้องการเปรียบเทียบการกระจายของข้อมูลตั้งแต่สองชุดขึ้นไปโดยแต่ละข้อมูลมีหน่วยวัดที่แตกต่างกัน หรือแต่ละข้อมูลมีค่าเฉลี่ยเลขคณิตแตกต่างกันมาก การนำค่าการกระจายมาเปรียบเทียบกันอาจจะทำให้เข้าใจผิดก็เป็นได้ เช่น ดูจากข้อมูล
ข้อมูลชุดที่ 1 ประกอบตัวเลข 1, 2, 5, 7, 9
ข้อมูลชุดที่ 2 ประกอบด้วยตัวเลข 129, 131, 134, 140, 143
จะพบว่าข้อมูลชุดที่ 1 จะมีค่าแตกต่างกันมาก ควรจะมีการกระจายมากกว่าข้อมูลชุดที่ 2 ซึ่งมีค่าแตกต่างกันน้อย แต่ถ้าวัดการกระจายของข้อมูลโดยใช้พิสัยจะได้
พิสัยของข้อมูลชุดที่ 1 = 9 – 1 = 8
พิสัยของข้อมูลชุดที่ 2 = 143 – 129 = 14
ถ้าดูจากพิสัยจะกลายเป็นว่าข้อมูลชุดที่ 2 มีการกระจายมากกว่าข้อมูลชุดที่ 1 ปัญหาเช่นนี้มักเกิดขึ้นเสมอ ดังนั้นจึงต้องสร้างตัวเลขที่จะใช้เปรียบเทียบข้อมูลขึ้นมาใหม่ในลักษณะของการกระจายสัมพันธ์ ค่าที่นิยมใช้คือ ค่าสัมประสิทธิ์ความผันแปร ดังนี้
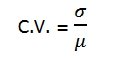
โดยข้อมูลใดมีค่า C.V. น้อย แสดงว่าข้อมูลชุดนั้นจะมีการกระจายต่ำซึ่งค่า C.V. อาจคำนวณเป็นรูปร้อยละก็ได้ กรณีนี้
![]()
ตัวอย่าง
สมมติผลการสอบวิชาสถิติ 111 ของนิสิต 2 กลุ่ม กลุ่มแรกได้แรกได้คะแนนเฉลี่ยเป็น 60 คะแนน และมีส่วนเบี่ยงเบนมาตรฐานเป็น 6 คะแนนส่วนกลุ่มที่สองได้คะแนนเฉลี่ยเป็น 70 คะแนน และมีส่วนเบี่ยงเบนมาตรฐานเป็น 10 คะแนน อยากทราบว่านิสิตกลุ่มใดสอบไล่วิชาสถิติ 111 ได้คะแนนกระจายน้อยที่สุด
วิธีทำ

เนื่องจากค่าสัมประสิทธิ์ความผันแปรของคะแนนสอบของนิสิตกลุ่มแรกต่ำกว่ากลุ่มที่สองดังนั้นนิสิตกลุ่มที่หนึ่งจะสอบได้คะแนนกระจายน้อยกว่านิสิตกลุ่มที่สอง
กลับไปที่เนื้อหา
วัตถุประสงค์ของการสุ่มตัวอย่างคือ นำเอาค่าวัดลักษณะของตัวอย่างไปทำการอนุมานค่าวัดลักษณะของประชากรที่ไม่ทราบค่า ตัวอย่างเช่นถ้าต้องการทราบค่าจ้างเฉลี่ยของคนงานไทย การหาค่าจ้างเฉลี่ยของคนงานไทยทั้งหมดได้ยาก เนื่องจากต้องเก็บรวบรวมค่าจ้างของคนงานทั้งหมดทำให้เสียค่าใช้จ่าย และเวลามาก ดังนั้นจึงมีความจำเป็นที่จะต้องใช้ข้อมูลจากตัวอย่างคือ ค่าจ้างเฉลี่ยของคนงานไทยบางส่วนไปทำการอนุมานค่าจ้างเฉลี่ยของคนงานไทยทั้งหมด
การอนุมานเชิงสถิติเป็นการใช้ข้อมูลจากตัวอย่างไปทำการสรุปผลหรือทำนายผลเกี่ยวกับค่าวัดลักษณะของประชากรหรือพารามิเตอร์ที่ไม่ทราบค่า ตัวอย่างเช่น ? และ ?2 แทนค่าเฉลี่ยและความแปรปรวนของประชากร ส่วน ![]() และ S2 แทนค่าเฉลี่ยและความแปรปรวนของตัวอย่างตามลำดับ เนื่องจากค่า
และ S2 แทนค่าเฉลี่ยและความแปรปรวนของตัวอย่างตามลำดับ เนื่องจากค่า ![]() และ S2 เป็นฟังก์ชันของตัวอย่างสุ่มและเรียกค่าเหล่านี้ว่า ค่าสถิติ (Statistic) ค่าสถิติจึงเป็นตัวแปรสุ่มที่ขึ้นอยู่กับตัวอย่าง ในกรณีของตัวแปรสุ่มใช้ภาษาอังกฤษตัวใหญ่อธิบายลักษณะของค่าสถิติ และภาษาอังกฤษตัวเล็กแทนค่าสังเกตของค่าสถิติ เช่น กรณีค่าเฉลี่ยตัวอย่างแทนค่าสถิติด้วย
และ S2 เป็นฟังก์ชันของตัวอย่างสุ่มและเรียกค่าเหล่านี้ว่า ค่าสถิติ (Statistic) ค่าสถิติจึงเป็นตัวแปรสุ่มที่ขึ้นอยู่กับตัวอย่าง ในกรณีของตัวแปรสุ่มใช้ภาษาอังกฤษตัวใหญ่อธิบายลักษณะของค่าสถิติ และภาษาอังกฤษตัวเล็กแทนค่าสังเกตของค่าสถิติ เช่น กรณีค่าเฉลี่ยตัวอย่างแทนค่าสถิติด้วย ![]() และค่าสังเกตของค่าสถิตินี้ด้วย
และค่าสังเกตของค่าสถิตินี้ด้วย ![]() สำหรับค่าความแปรปรวนของตัวอย่างแทนค่าสถิติด้วย S2 และแทนค่าสังเกตของค่าสถิติด้วย s2
สำหรับค่าความแปรปรวนของตัวอย่างแทนค่าสถิติด้วย S2 และแทนค่าสังเกตของค่าสถิติด้วย s2
ค่าสถิติสามารถคำนวณได้จากข้อมูลตัวอย่างกล่าวคือ ถ้า X1, X2 ,…, Xn แทนค่าข้อมูลตัวอย่าง n ค่า
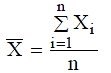
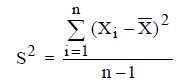
ในประชากรหนึ่งๆ ค่าสถิติแต่ละค่าขึ้นอยู่กับตัวอย่างที่เราสุ่มได้ ค่าสถิติมีได้หลายค่า ดังนั้นค่าสถิติเป็นค่าของตัวแปรเชิงสุ่มที่สามารถหาการแจกแจงความน่าจะเป็นได้ การแจกแจงความน่าจะเป็นของค่าสถิตินี้เรียกว่า การแจกแจงตัวอย่าง (Sampling distribution) ตัวอย่างเช่น การแจกแจงความน่าจะเป็นของ ![]() เรียกว่า การแจกแจงตัวอย่างของค่าเฉลี่ย และสำหรับค่าเบี่ยงเบนมาตรฐานของการแจกแจงของตัวอย่างเรียกว่า ความคลาดเคลื่อนมาตรฐาน (Standard Error) ของค่าสถิติ เช่น ความคลานเคลื่อนมาตรฐานของค่าเฉลี่ยคือค่าเบี่ยงเบนมาตรฐานของค่าเฉลี่ยคือ ค่าเบี่ยงเบนมาตรฐานของการแจกแจงตัวอย่างของ
เรียกว่า การแจกแจงตัวอย่างของค่าเฉลี่ย และสำหรับค่าเบี่ยงเบนมาตรฐานของการแจกแจงของตัวอย่างเรียกว่า ความคลาดเคลื่อนมาตรฐาน (Standard Error) ของค่าสถิติ เช่น ความคลานเคลื่อนมาตรฐานของค่าเฉลี่ยคือค่าเบี่ยงเบนมาตรฐานของค่าเฉลี่ยคือ ค่าเบี่ยงเบนมาตรฐานของการแจกแจงตัวอย่างของ ![]() นั่นเอง
นั่นเอง
กลับไปที่เนื้อหา
การแจกแจงความน่าจะเป็นของตัวแปรสุ่ม![]()

ประชากรมีค่าเฉลี่ย ? = 10
สุ่มตัวอย่างขนาด n = 15 ทำการทดลองทั้งหมด 1000 ชุด
ตัวอย่างได้ค่าเฉลี่ยตัวอย่างเป็น![]()
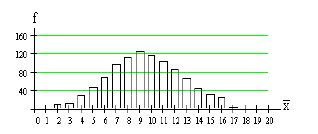
สุ่มตัวอย่างขนาด n = 50 ทำการทดลองทั้งหมด 1000 ชุด
ตัวอย่างได้ค่าเฉลี่ยตัวอย่างเป็น![]()
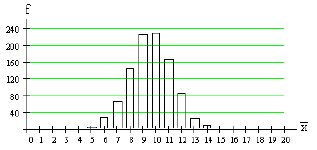
สุ่มตัวอย่างขนาด n = 100 ทำการทดลองทั้งหมด 1000 ชุด
ตัวอย่างได้ค่าเฉลี่ยตัวอย่างเป็น![]()
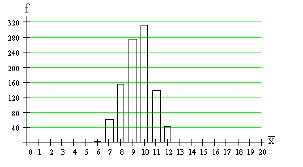
กลับไปที่เนื้อหา
ค่าเฉลี่ยเลขคณิตของ ![]() และ ความแปรปรวนของ
และ ความแปรปรวนของ ![]() กรณีสุ่มตัวอย่างออกมาพร้อมกัน
กรณีสุ่มตัวอย่างออกมาพร้อมกัน
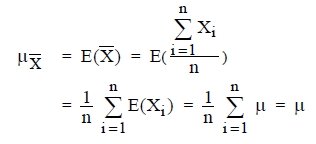
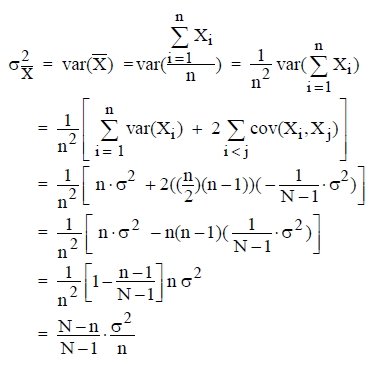
เมื่อขนาดของประชากร N มีค่ามาก หรือการสุ่มตัวอย่างกระทำโดยการหยิบแล้วใส่คืนกับที่เดิมจะได้
ค่าเฉลี่ยของค่าเฉลี่ย![]()
และค่าความแปรปรวนของค่าเฉลี่ย![]()
ทฤษฎีบท (The Central Limit Theorem)
ถ้า X เป็นค่าเฉลี่ยเลขคณิตของตัวอย่างสุ่มขนาด n จาก ประชากรซึ่งมีค่าเฉลี่ยเลขคณิต ? และความแปรปรวน ?2แล้วการแจกแจงของตัวแปรสุ่ม 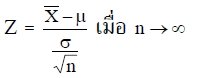
จะประมาณได้ด้วยการแจกแจงปกติมาตรฐาน n(z ; 0 , 1)
หมายเหตุ
1. ถ้า n < 30 การประมาณการแจกแจงนี้จะให้ผลดี ก็ต่อเมื่อประชากรมีการแจกแจงใกล้เคียงกับการแจกแจงปกติ
2. ถ้าประชากรมีการแจกแจงปกติแล้ว การแจกแจงของค่าเฉลี่ย เลขคณิตของตัวอย่างก็จะมีการแจกแจงปกติ โดยไม่คำนึงถึงขนาดของตัวอย่างว่าจะมากน้อยเพียงไร
กลับไปที่เนื้อหา



