ฟังก์ชัน
ความสัมพันธ์ที่เป็นฟังก์ชัน
การตรวจสอบความสัมพันธ์ที่เป็นฟังก์ชัน สามารถทำได้โดยใช้บทนิยามของฟังก์ชัน
นิยามฟังก์ชัน คือ ความสัมพันธ์ซึ่งในสองคู่อันดับใด ๆ ของความสัมพันธ์นั้น ถ้ามีสมาชิกตัวหน้าเท่ากันแล้ว
สมาชิกตัวหลังต้องไม่ต่างกัน
การตรวจสอบความสัมพันธ์ที่กำหนดให้ในรูปแบบแจกแจงสมาชิก สามารถทำได้ดังตัวอย่างต่อไปนี้
ตัวอย่างที่ 1จงตรวจสอบว่าความสัมพันธ์ต่อไปนี้เป็นฟังก์ชันหรือไม่
f = {(0,1),(2,3),(4,5),(0,2)}
g ={(1,2),(7,8),(5,9),(1,2)}
จากความสัมพันธ์ที่กำหนดให้จะพบว่าทั้ง f และ g ต่างมีคู่อันดับที่มีสมาชิกตัวหน้าซ้ำกัน คือ (0,1) กับ (0,2) และ (1,2) กับ (1,2) ตามลำดับ แต่สมาชิกตัวหลังของคู่อันดับที่ซ้ำกันใน f ไม่เหมือนกัน ดังนั้น f จึงไม่เป็นฟังก์ชัน แต่ g เป็นฟังก์ชัน
สำหรับความสัมพันธ์ที่กำหนดมาในรูปแบบบอกเงื่อนไข สามารถตรวจสอบได้ 2 วิธีคือ
1.ตรวจสอบโดยใช้บทนิยามให้นำสมการแสดงความสัมพันธ์ระหว่างสมาชิกตัวหน้า x กับสมาชิกตัวหลัง y มาตรวจสอบค่า y ที่ได้จากค่า x หนึ่ง ๆ หากมีค่า y ที่เป็นไปได้เพียงค่าเดียว ความสัมพันธ์นั้นจะเป็นฟังก์ชัน
ตัวอย่างที่ 2จงตรวจสอบว่าความสัมพันธ์ f = {(x,y)ϵR x R | y2= x + 1} เป็นฟังก์ชันหรือไม่
วิธีทำพิจารณาค่าของสมาชิกตัวหลัง y1และ y2ที่ค่าสมาชิกตัวหน้าเดียวกัน x
จะได้
y12= x + 1 ---------- (1)
y22= x + 1 ---------- (2)
ด้านขวามือของสมการทั้งสองเท่ากัน ดังนั้น
y12=y22หรือy1= ± y2
จะพบว่าy1ไม่จำเป็นต้องเท่ากับy2
นั่นคือ f ไม่เป็นฟังก์ชัน
ตัวอย่างที่ 3จงตรวจสอบว่าความสัมพันธ์ gเป็นฟังก์ชันหรือไม่ เมื่อ
![]()
วิธีทำโดยวิธีการเดียวกับตัวอย่างที่ 2 จะได้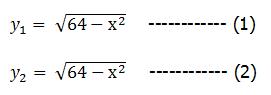
นำ (1) = (2) ได้ ![]()
หรือy1=y2
นั้นคือ g เป็นฟังก์ชัน
2.ตรวจสอบจากการวาดกราฟวิธีนี้ทำได้โดยลากเส้นตรงขนานแกน y ลงบนกราฟของความสัมพันธ์ หากไม่มี
เส้นตรงใดตัดกราฟของความสัมพันธ์มากกว่า 1 จุด ความสัมพันธ์นั้นจะเป็นฟังก์ชัน แต่ถ้ามีอย่างน้อย 1 เส้นตัด
กราฟ 2 จุด ความสัมพันธ์นั้นจะไม่เป็นฟังก์ชัน
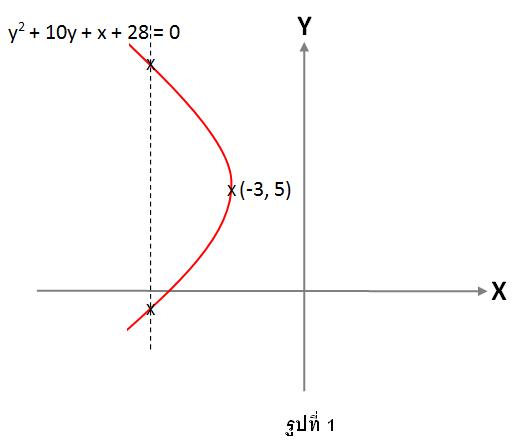
ตัวอย่างที่ 4f = {(x,y)ϵR x R | y2+ 10y + x + 28 = 0} จงหาว่า f เป็นฟังก์ชันหรือไม่
วิธีทำ1. จัดรูปสมการ เพื่อเขียนกราฟได้
y2+ 10y + x + 28 = 0
y2+ 10y + 25 = -x - 28 + 25
(y-5)2= - (x+3)
2. วาดกราฟ สมการที่ได้เป็นสมการพาราโบลา เปิดทางด้านซ้าย ซึ่งมีจุดยอดอยู่ที่ (-3,5) ซึ่งมีกราฟดังรูปที่ 1
เมื่อลากเส้นขนานแกน y จะพบว่ามีเส้นตรงตัดกราฟ 2 จุด ดังนั้นจึงสรุปได้ว่า f ไม่เป็นฟังก์ชัน
กลับไปที่เนื้อหา
การหาโดเมนและเรนจ์ของความสัมพันธ์จากการวาดกราฟขั้นพื้นฐาน
การหาโดเมนและเรนจ์ของความสัมพันธ์สามารถทำได้อย่างง่ายยิ่งขึ้น ถ้าสามารถวาดกราฟของความสัมพันธ์ที่กำหนดให้ได้ การหาโดเมนทำได้โดยการพิจารณากราฟในส่วนที่ครอบคลุมแกน x และการหาเรนจ์ทำได้โดยพิจารณากราฟในส่วนที่ครอบคลุมแกน y การวาดกราฟส่วนใหญ่จะใช้ความรู้พื้นฐานทางเรขาคณิตวิเคราะห์ และภาคตัดกรวยกราฟที่จะพิจารณาต่อไปนี้จะเป็นกราฟค่าสัมบูรณ์ และกราฟอื่น ๆ ที่เกี่ยวข้อง
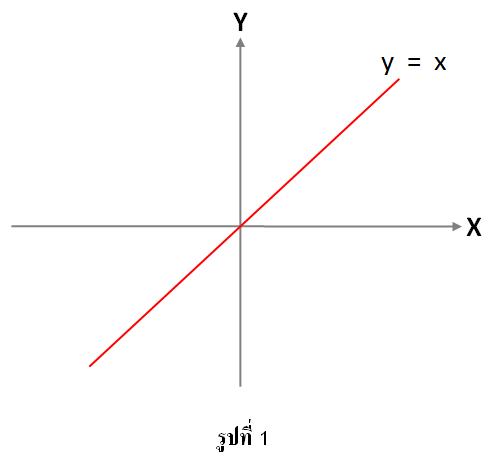
1. y = x ซึ่งเป็นสมการเส้นตรง ดังรูป
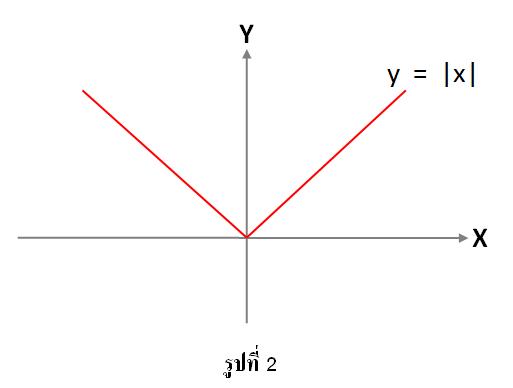
สำหรับสมการ y = |x| จะพบว่า x เป็นได้ทั้งค่าบวกและค่าลบ ส่วน y จะเป็นบวกเสมอ และมีจุดยอด คือ (0,0)ซึ่งกราฟที่ได้ จะได้จากการกลับค่าของ y จากส่วนที่เป็นลบในกราฟy = x ขึ้นมาเป็นค่าบวก ดังรูปที่ 2 ดังนั้น โดเมน คือ จำนวนจริง และ เรนจ์ คือ [0,∞)
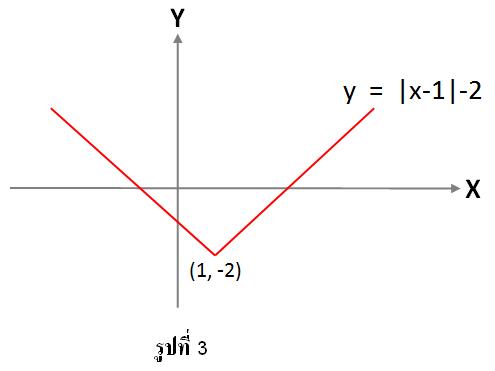
2. y = |x - 1| - 2 หรือจัดรูปใหม่ได้เป็นy + 2 = |x - 1| ในกรณีนี้กราฟที่ได้ยังคงเหมือนเดิมแต่มีจุดยอดคือ (h,k) = (1,-2) กราฟที่ได้จะเป็นการเลื่อนกราฟในตำแหน่งของจุดยอดอยู่ที่ (1,-2) ดังรูปที่ 3
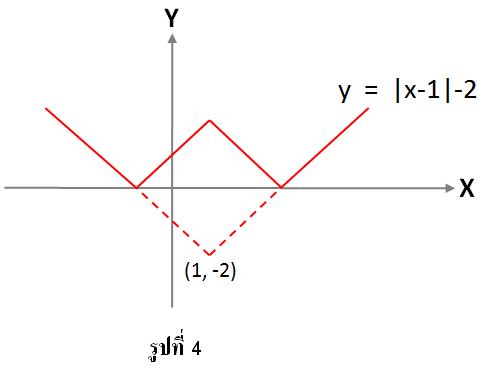
3. y = ||x-1|-2| มีการเพิ่มค่าสัมบูรณ์จากข้อ 2 ดังนั้น ให้พิจารณาเหมือนข้อ 2 ก่อน คือ
y = |x - 1| - 2 จัดรูปใหม่เป็นy + 2 = |x - 1| จะได้กราฟเหมือนข้อ 2 แต่เมื่อเพิ่มค่าสัมบูรณ์อีกชั้นหนึ่ง
จะได้y = ||x-1|-2| การวาดกราฟของสมการy = ||x-1|-2| ทำได้โดยการกลับค่า y ที่เป็นลบ ของสมการ
y = |x - 1| - 2 ขึ้นมาเป็นค่าบวกดังรูปที่ 4
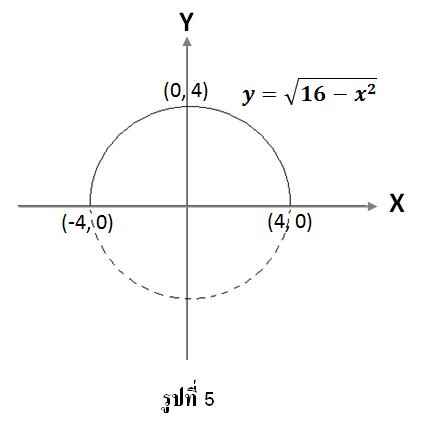
4.จากสมการ y เป็นบวกเสมอ เมื่อยกกำลังสองทั้งสองข้างจะได้สมการวงกลม รัศมี 4 คือ
x2+ y2= 16กราฟที่ได้จะเป็นครึ่งวงกลมเฉพาะส่วนที่อยู่เหนือแกน x เนื่องจาก y เป็นลบไม่ได้ ดังรูปที่ 5
กลับไปที่เนื้อหา
การหาโดเมนและเรนจ์ของความสัมพันธ์จากการวาดกราฟขั้นประยุกต์
การหาโดเมนและเรนจ์ของความสัมพันธ์ โดยการวาดกราฟจะมีความซับซ้อนมากขึ้นเมื่อมีการกำหนดเงื่อนไข และการที่ความสัมพันธ์อยู่ในรูปของอสมการ ทำให้กราฟที่กำลังพิจารณาเป็นบริเวณที่ได้จากอสมการนั้น ๆ นอกเหนือจากเส้นกราฟ การหาโดเมนและเรนจ์ทำได้ดังตัวอย่างต่อไปนี้
1. กรณีมีการกำหนดเงื่อนไข เช่น ให้![]()
จากโจทย์ ควรจัดรูปสมการใหม่ เพื่อดูว่าเป็นกราฟอะไร ในกรณีนี้จะได้สมการใหม่เป็น
(x-2)2= -12(y-5) ------- (1)
ดังนั้นเป็นสมการพาราโบลาที่มีแกนพาราโบลาขนานแกน y เนื่องจากกำลังสองอยู่ที่ x และเป็นแกนพาราโบลาคว่ำ เนื่องจากสัมประสิทธหน้า y เป็นเครื่องหมายลบ ซึ่งสามารถเขียนกราฟได้ดังรูปที่ 1 แต่เงื่อนไขของโจทย์ y ต้องเป็นจำนวนจริงบวก ดังนั้นกราฟที่ได้จึงเป็นกราฟรูปที่ 2
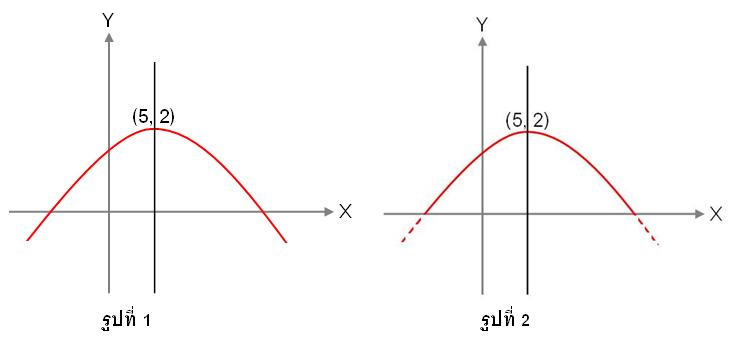
โดเมนของความสัมพันธ์นี้หาได้จากค่าของ x ในช่วงนี้นิยมค่า y นั่นคือ ระหว่างจุดตัดแกน x ทั้ง 2 ค่า
เมื่อให้ y = 0 จะได้
x2- 4x + 4 = -12(0-5)
x2- 4x - 56 = 0 หรือ
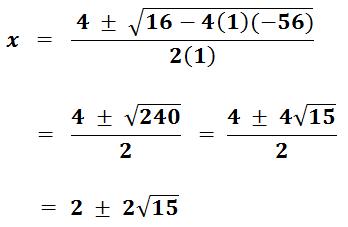
ดังนั้น โดเมนของความสัมพันธ์คือ![]()
ส่วนเรนจ์ของความสัมพันธ์สามารถหาได้จากกราฟโดยตรง ซึ่งจะได้เรนจ์ของความสัมพันธ์คือ (0,2]
2. กรณีวาดกราฟในรูปอสมการ เช่น![]()
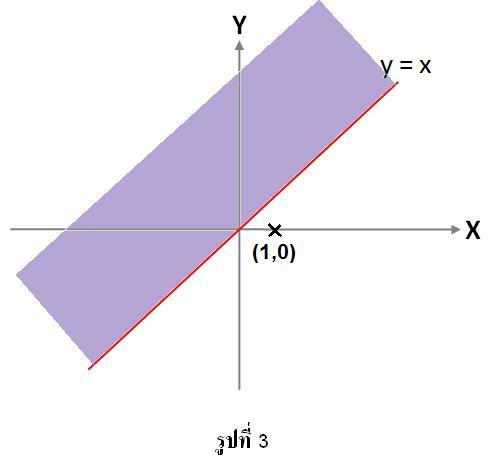
จาก y ≥ x ให้วาดกราฟ y = x ก่อนดังรูปที่ 3 จากนั้นเลือกจุดคู่อันดับง่าย ๆ ของแต่ละบริเวณแทนลงไป
เพื่อดูว่าความสัมพันธ์ดังกว่าเป็นจริงในช่วงใด เช่นเลือก (1,0) แทนลงไปในอสมการ y ≥ x จะได้ 0 ≥ 1
ซึ่งทำให้อสมการไม่เป็นจริงดังนั้น ควรแรเงาอีกด้านหนึ่งของกราฟเส้นตรง คนละด้านกับจุด (1,0) ดังรูปที่ 3
จากนั้นวาดกราฟ y2≥ 4x โดยเรายังไม่ต้องคำนึงถึงเครื่องหมายของอสมการ แต่ให้วาดกราฟ y2= 4x ขึ้นมา
ก่อน ดังรูปที่ 4 จากนั้นสุ่มเลือกจุดง่าย ๆ เพื่อดูว่าต้องแรเงาช่วงใดที่ทำให้อสมการเป็นจริง เช่น เลือกจุด (1,0)
แทนลงในอสมการ y2≤ 4x จะได้ 0 ≤ 4(1) ซึ่งทำให้อสมการเป็นจริง ดังนั้นควรแรเงากราฟในบริเวณที่จุด
(1,0) อยู่ ดังรูปที่ 4 จากนั้น นำกราฟที่ได้จากการแรเงาของอสมการทั้ง 2 มาอินเตอร์เซกกัน ดังรูปที่ 5
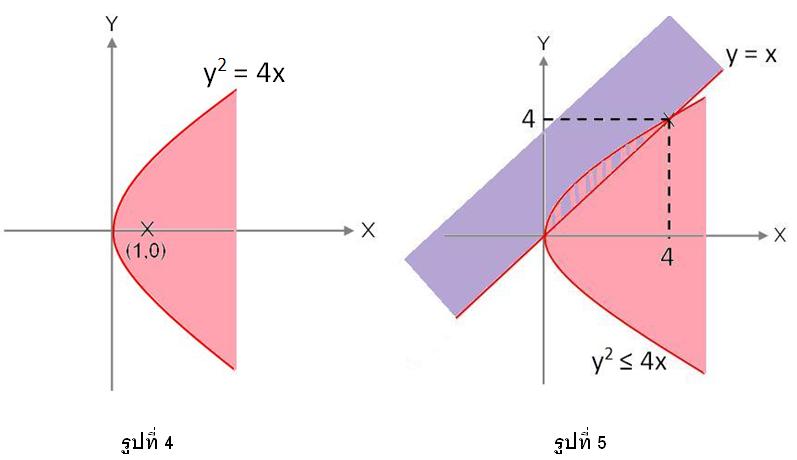
การหาโดเมนและเรนจ์จะพิจารณาเฉพาะช่วงที่อินเตอร์เซกกันเท่านั้น ซึ่งเป็นบริเวณที่อยู่ระหว่างจุดตัดของกราฟเส้นตรงและพาราโบลา การหาจุดตัดของสมการทำได้โดยการแก้สมการ
y2= 4x ---------(2)
x = y---------(3)
แทน สมการที่ (3) ลง สมการที่ (2) จะได้
x2- 4x = 0
x(x-4) = 0
ดังนั้น x = 0, 4 เนื่องจาก x = y จากสมการที่ (3) จึงได้ว่าสมการทั้งสองตัดกันที่จุด (0,0), (4,4)
จากรูปที่ 5 จะพบว่า โดเมนอยู่ในช่วง [4,0] และเรนจ์อยู่ในช่วง [0,4]
กลับไปที่เนื้อหา
การหาโดเมนและเรนจ์ของความสัมพันธ์จากการแก้สมการ
ในกรณีที่สมการอยู่ในรูปแบบที่เขียนกราฟไม่ได้หรือการเขียนกราฟทำได้ยากและเสียเวลา การหา
โดเมนและเรนจ์ สามารถทำได้จากสมการแสดงความสัมพันธ์ได้ดังนี้
การหาโดเมนให้จัดรูปสมการ ให้ y อยู่ในรูปของ x และพิจารณาค่า x ที่เป็นไปได้ทั้งหมดที่ทำ
ให้ y สามารถหาค่าได้ เช่น xy - x = 5 ให้เราจัดรูป เป็น y = (x+5)/x จากสมการจะพบว่า ทุก
ค่า x สามารถหาค่า y ได้เสมอ โดเมนของสมการนี้คือ![]()
การหาเรนจ์ให้จัดรูปสมการให้ x อยู่ในรูปของ y และพิจารณาค่า y ทุกค่าที่ทำให้ x สามารถหา
ค่าได้ ดังตัวอย่างต่อไปนี้
ตัวอย่างที่ 1ให้ ![]() จงหาเรนจ์ของความสัมพันธ์ r
จงหาเรนจ์ของความสัมพันธ์ r
วิธีที่ 1จากสมการจะพบว่า y ≥ 0 เสมอ จัดรูปสมการให้ x อยู่ในรูปของ y โดยการยกกำลัง
สองทั้ง 2 ข้าง
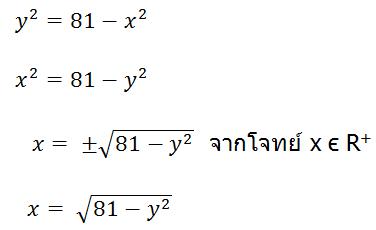
จากสมการจะพบว่า ภายใต้เครื่องหมายราก ที่จะทำให้ x เป็นจริงได้ต้องมากกว่า หรือเท่ากับศูนย์ ดังนั้น
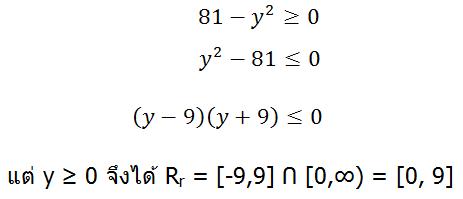
วิธีที่ 2จากสมการ
ตัวอย่างที่ 2ให้![]() จงหาโดเมนและเรนจ์
จงหาโดเมนและเรนจ์
วิธีทำการหาโดเมนทำได้โดย พิจารณาค่า x ที่เป็นไปได้ เริ่มจาก![]() ซึ่งจะหาค่าได้เมื่อ
ซึ่งจะหาค่าได้เมื่อ
7-x ≥ 0 หรือ
x-7 ≤ 0 นั่นคือx≤ 7และ
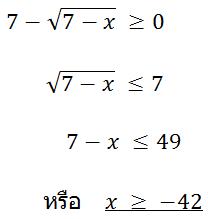
ดังนั้น โดเมนของ r คือ [-42,7]
การหาเรนจ์
กลับไปที่เนื้อหา
ความสัมพันธ์ที่เป็นฟังก์ชันจาก A ไป B
บทนิยามf เป็นฟังก์ชันจาก A ไป B ก็ต่อเมื่อ f เป็นฟังก์ชันที่มี A เป็นโดเมน และมีสับเซตของ B เป็นเรนจ์
f เป็นฟังก์ชันจาก Aไป B เขียนแทนด้วย f : A → B
จากนิยามข้างต้น จะพบว่าเมื่อมีการจับคู่ระหว่างสมาชิกของเซต A และ เซต B แล้ว สมาชิกของเซต A ต้องใช้ในการจับคู่ทุกตัว แต่สมาชิกในเซต B ไม่จำเป็นต้องใช้ในการจับคู่ทุกตัว หรือกล่าวอีกอย่างหนึ่งว่าโดเมนจะต้องเท่ากับเซต A และ เรนจ์จะเป็นสับเซตของ B ดังตัวอย่างต่อไปนี้
ตัวอย่างที่ 1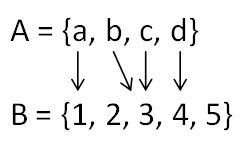
จากแผนภาพจะพบว่า โดเมน คือ A
และ เรนจ์ คือ {1, 3, 4} ซึ่งเป็นซับเซตของ B
f : A → B คือ {(a,1), (b,3), (c,3), (d,4)}
ความสัมพันธ์ที่เป็นฟังก์ชันจาก A ไปทั่วถึง B
กรณีที่โดเมนชองฟังก์ชันคือ A และ เรนจ์ของฟังก์ชันคือ B เรียกฟังก์ชันที่มีสมบัตินี้ว่า ฟังก์ชันจาก A ไปทั่วถึง B มีนิยามดังนี้
บทนิยาม f เป็นฟังก์ชันจาก A ไปทั่วถึง B ก็ต่อเมื่อ f เป็นฟังก์ชันที่มี A เป็นโดเมน และ B เป็นเรนจ์
fเป็นฟังก์ชันจาก A ไปทั่วถึง B เขียนแทนด้วย![]()
จากนิยาม สรุปได้ว่าสมาชิกทุกตัวของ A และ B เกี่ยวข้องในความสัมพันธ์นี้
ตัวอย่างที่ 2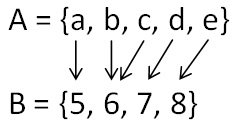
ในตัวอย่างนี้ โดเมน คือ A
และเรนจ์ คือ B![]() คือ {(a,5), (b,6), (c, 6), (d,7), (e,8)}
คือ {(a,5), (b,6), (c, 6), (d,7), (e,8)}
ความสัมพันธ์ที่น่าสนใจอีกแบบหนึ่งคือ ความสัมพันธ์ที่มีการเขียนคู่อันดับโดยใช้สมาชิกตัวหน้า และตัวหลังในเซตเดียวกัน กล่าวคือ ถ้า r เป็นความสัมพันธ์จาก A ไป A เรียก r ว่าเป็นความสัมพันธ์ใน Aดังตัวอย่างต่อไปนี้
ตัวอย่างที่ 3 ให้ A = {w, x, y, z}
และ r = {(x,y), (y,z), (w,x), (z,w)}
จะเรียก r ว่าเป็นความสัมพันธ์ใน A
กลับไปที่เนื้อหา
ตัวอย่างฟังก์ชันที่ควรรู้จัก
1)ฟังก์ชันเชิงเส้นคือ ฟังก์ชันที่อยู่ในรูป f(x) = mx + c เมื่อ m และ c เป็นจำนวนจริง เช่น
f(x) = 3x + 4
f(x) = -2x + 1
เมื่อ m = 0 จะได้ฟังก์ชันอยู่ในรูป f(x) = cฟังก์ชันนี้มีชื่อเรียกเฉพาะว่าฟังก์ชันคงตัว กราฟจะเป็นเส้นตรงขนานแกน x
ในกรณีทั่วไปจะได้กราฟเส้นตรงที่มีความชันเท่ากับ m และตัดแกน y ที่จุด (0, c)
2)ฟังก์ชันขั้นบันไดคือ ฟังก์ชันที่มีโดเมนเป็นสับเซตของ R และมีค่าฟังก์ชันคงตัวเป็นช่วง ๆ มากกว่า 2 ช่วง กราฟของฟังก์ชันนี้มีรูปคล้ายขั้นบันได ตัวอย่างเช่น การตัดเกรดของนักศึกษา
ตัวอย่างที่ 1การตัดเกรดในช่วงคะแนนในระดับต่าง ๆ เป็นดังนี้
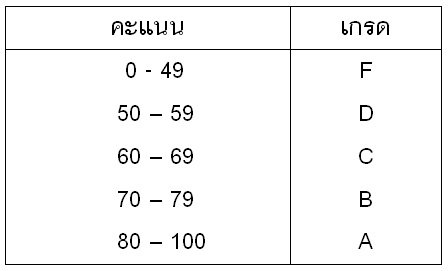
จงเขียนกราฟแสดงฟังก์ชัน และเขียนฟังก์ชันในรูป f(x) เมื่อ x เป็นคะแนน และ f(x) เป็นเกรด
วิธีทำ
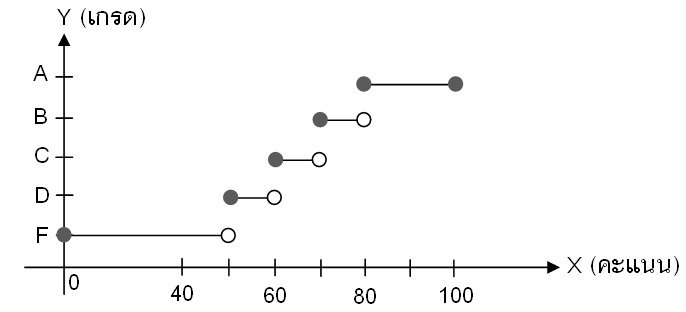
ฟังก์ชันนี้เขียนในรูปสมการได้ดังนี้
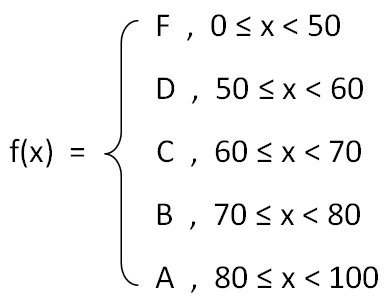
ให้สังเกตว่าที่ค่า x เดียวกันจะไม่มีค่า y มากกว่า 1 ค่า ซึ่งเป็นไปตามบทนิยามของความสัมพันธ์ที่เป็นฟังก์ชัน
3)ฟังก์ชันกำลังสองคือฟังก์ชันที่อยู่ในรูป f(x) = ax2+ bx + c เมื่อ a, b, c เป็นจำนวนจริงใด ๆ และ
a≠ 0 ค่า a ที่เป็นบวก หรือ ลบ จะให้กราฟรูปพาราโบลาหงาย หรือ คว่ำ ถ้า a = 0 จะได้ฟังก์ชันคงตัว
กลับไปที่เนื้อหา



