การหมุน
คอนเซปต์หลักในการหมุน

การเคลื่อนที่แนววงกลมที่ผ่านมาคิดเสมือนว่ามวลของวัตถุรวมอยู่ที่จุดเล็กๆ จุดหนึ่ง ซึ่งในความจริงวัตถุไม่ได้อยู่เป็นจุด แต่มีทั้งขนาดและปริมาตร โดยการหมุนจะต่างจากการเคลื่อนที่แนววงกลมตรงที่ว่า การเคลื่อนที่แนววงกลมคือการที่จุดวัตถุเคลื่อนที่เป็นวงกลมรอบจุดศูนย์กลาง ส่วนการเคลื่อนที่แบบหมุนคือการที่ก้อนวัตถุเคลื่อนที่เป็นวงกลมรอบจุดศูนย์กลาง ส่วนการเคลื่อนที่แบบหมุน คือการที่ก้อนวัตถุเคลื่อนที่เป็นงกลมรอบแกนหมุน เช่น ลูกข่าง พัดลม ล้อรถ เป็นต้นเมื่อก้อนวัตถุหมุนรอบแกนหมุน เราสามารถมองได้ว่าก้อนวัตถุเกิดจากจุดอนุภาควัตถุหลาย ๆ จุดมารวมกัน ซึ่งแต่ละจุดมีความเร็วและความเร่งเป็นค่าเฉพาะของตัวมันเอง ฉะนั้นเราไม่สามารถวิเคราะห์การเคลื่อนที่แยกทีละจุดได้ และเราจะวิเคราะห์ก้อนวัตถุทั้งหมดรวมกันแทน

ในการวิเคราะห์วัตถุที่กำลังหมุน เรามักกำหนดให้วัตถุนั้นเป็นวัตถุเกร็ง ซึ่งหมายถึงวัตถุที่ไม่สามารยืดหดได้ ดังนั้นเมื่อวัตถุหมุนแต่ละจุดบนวัตถุจะยึดติดกันไปเสมอ ทำให้ทุกจุดหมุนด้วยความเร็วเชิงมุม ω เท่ากัน ทั้งวัตถุอาจหมุนด้วยความเร็วเชิงมุมเพิ่มขึ้นหรือลดลงก็ได้ เราเรียกอัตราการเปลี่ยนแปลง ω ว่าความเร่งเชิงมุม (α) ซึ่งต่างจากความเร่งเชิงเส้น (a)
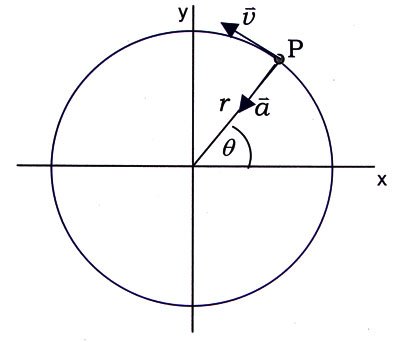
ถ้าดูแต่ละจุด และมองให้จุดที่เราสนใจเสมือนเคลื่อนที่เป็นแนววงกลมด้วย ความเร็วเชิงเส้น v จะพบว่า v= ωr เหมือนในเรื่องการเคลื่อนที่แนววงกลม เมื่อ r คือระยะห่างระหว่างจุดที่สนใจกับแกนหมุน อย่างไรก็ตาม ในเมื่อทุกจุดมี ω เท่ากัน แต่ค่า r ไม่เท่ากัน ก็จะทำให้แต่ละจุดมี v ต่างกันด้วย (บางจุดอาจมีระยะห่างเท่ากัน อัตราเร็วเชิงเส้นก็อาจจะเท่ากัน แต่ไม่ใช่ว่าทุกจุดจะเท่ากัน) สามารถสรุปเป็นสูตรได้ดังนี้1. s = Ɵr2. v = ωr3. a =αr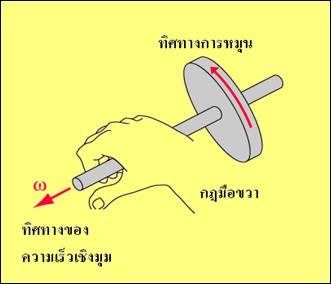
เราสามารถเขียนความเร็วเชิงมุม และความเร่งเชิงมุมในรูปเวกเตอร์ คือ![]() และ
และ![]() ซึ่งมีทิศทาง แต่ในเรื่องการหมุนจะมีนิยามพิเศษอยู่ว่า ทิศของความเร็วเชิงมุม
ซึ่งมีทิศทาง แต่ในเรื่องการหมุนจะมีนิยามพิเศษอยู่ว่า ทิศของความเร็วเชิงมุม![]() ไม่ใช่แนวการหมุนจริงๆของวัตถุ และทิศของความเร่งเชิงมุม
ไม่ใช่แนวการหมุนจริงๆของวัตถุ และทิศของความเร่งเชิงมุม![]() ก็ไม่ใช่แนวความเร่งจริงๆของวัตถุด้วยในการหาทิศให้ใช้มือขวาของน้อง โดยใช้สี่นิ้ววนไปรอบทิศของการหมุน นิ้วโป้งจะชี้ไปในทิศ
ก็ไม่ใช่แนวความเร่งจริงๆของวัตถุด้วยในการหาทิศให้ใช้มือขวาของน้อง โดยใช้สี่นิ้ววนไปรอบทิศของการหมุน นิ้วโป้งจะชี้ไปในทิศ![]() และถ้าต้องการหาทิศ
และถ้าต้องการหาทิศ![]() ให้พิจารณาความเร็วเชิงมุมของการหมุน
ให้พิจารณาความเร็วเชิงมุมของการหมุน![]() ถ้า
ถ้า![]() มากขึ้น (หมุนเร็วขึ้น)
มากขึ้น (หมุนเร็วขึ้น)![]() จะมีทิศเดียวกับ
จะมีทิศเดียวกับ![]() แต่ถ้า
แต่ถ้า![]() น้อยลง (หมนุช้าลง)
น้อยลง (หมนุช้าลง)![]() จะมีทิศตรงข้ามกับ
จะมีทิศตรงข้ามกับ![]() เพราะ
เพราะ![]()
กลับไปที่เนื้อหา
การขจัดเชิงมุม ความเร็ว และความเร่ง
(Angular displacement velocity and acceleration)
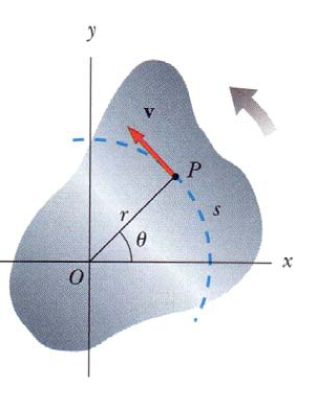
จากรูปแสดงวัตถุแข็งเกร็งลักษณะบางมีรูปร่างใด ๆ ในระนาบ xy หมุนรอบแกนที่อยู่กับที่ที่ผ่านจุด O โดยแกนจะตั้งฉากกับระนาบ xy พิจารณาการเคลื่อนที่ของอนุภาคเพียงอนุภาคเดียวที่จุด P ซึ่งอยู่ห่างจากจุดกำเนิด O เป็นระยะ r และเคลื่อนที่รอบแกนเป็นวงกลมรัศมี r (อนุภาคทุกอนุภาคบน วัตถุแข็งเกร็งจะเคลื่อนที่รอบจุด O เป็นวงกลม)เพื่อความสดวกจึงใช้การกำหนดพิกัดของอนุภาคโดยใช้พิกัดเชิงขั้ว (r,q) โดยการวัดมุม q ทวนเข็มนาฬิกาเริ่มจากทางแกนบวก x จะพบว่ามุม q มีการเปลี่ยนแปลงเทียบกับเวลา แต่ r มีค่าคงที่ (ในระบบพิกัดฉาก x และ y มีการเปลี่ยนแปลงเทียบกับเวลา ) เมื่ออนุภาคเคลื่อนที่ไปยังจุด P มันจะเคลื่อนที่ได้ส่วนโค้ง (arc) s ซึ่งมีความสัมพันธ์กับตำแหน่งเชิงมุม q (radian : rad) ดังนี้การวัดค่ามุม Ɵ ที่เป็นธรรมชาติที่สุด คือการวัดในหน่วยเรเดียน (rad)1 รอบวงกลม = 2 ¶ เรเดียนถ้าวัตถุมีการหมุนรอบแกน z ซึ่งเป็นแนวที่ตั้งฉากกับระนาบกระดาษ ตำแหน่งเชิงมุมของวัตถุจะมีการเปลี่ยนแปลงไป (เมื่อใช้จุด p เป็นตัวแทนของวัตถุ)จะทำให้เกิดการกระจัดเชิงมุม![]() ในช่วงเวลา
ในช่วงเวลา![]() - ขนาดความเร็วเชิงมุมเฉลี่ยของวัตถุหาได้จาก
- ขนาดความเร็วเชิงมุมเฉลี่ยของวัตถุหาได้จาก![]() - ขนาดความเร็วเชิงมุมขณะใดขณะหนึ่งของวัตถุ
- ขนาดความเร็วเชิงมุมขณะใดขณะหนึ่งของวัตถุ![]() ถ้าเราหาการเปลี่ยนแปลงความเร็วเชิงมุมขณะใดขณะหนึ่ง เราจะได้ปริมาณที่เรียกว่า ความเร่งเชิงมุม (อ่านว่า อัลฟา)- ความเร่งเชิงมุมเฉลี่ยของวัตถุหาได้จาก
ถ้าเราหาการเปลี่ยนแปลงความเร็วเชิงมุมขณะใดขณะหนึ่ง เราจะได้ปริมาณที่เรียกว่า ความเร่งเชิงมุม (อ่านว่า อัลฟา)- ความเร่งเชิงมุมเฉลี่ยของวัตถุหาได้จาก![]()
- ความเร่งเชิงมุมขณะใดขณะหนึ่ง หาได้จาก![]()
เนื่องจากความเร็วเชิงมุม และความเร่งเชิงมุมต่างก็เป็นปริมาณเวกเตอร์เราสามารถหาทิศของความเร็วเชิงมุมได้จากกฎมือขวาโดยกำนิ้วทั้งสี่ไปในทิศที่วัตถุกำลังหมุน ทิศที่นิ้วหัวแม่มือชี้ไปแสดงถึงทิศทางของความเร็วเชิงมุม
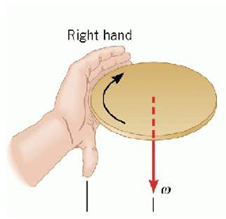
เวกเตอร์ของความเร่งเชิงมุมจะมีทิศทางเดียวกับทิศทางของความเร็วเชิงมุมก็ต่อเมื่อขนาดของความเร็วเชิงมุมเพิ่มขึ้นและความเร่งเชิงมุมจะมีทิศทางตรงข้ามกับทิศทางของความเร็วเชิงมุม เมื่อขนาดของความเร็วเชิงมุมลดลง
การหมุนด้วยความเร่งเชิงมุมคงตัวถ้าการหมุนของวัตถุมีความเร็วเชิงมุมต้นที่เวลา t = 0 เป็น![]() ที่เวลา t ใด ๆ มี
ที่เวลา t ใด ๆ มี![]() มีความเร็วเชิงมุมเป็น ในช่วงเวลานั้นความเร่งเชิงมุมคงที่เท่ากับ จะได้สมการการเคลื่อนที่แบบหมุน เมื่อพิจารณาขนาดของปริมาณต่าง ๆ จะได้
มีความเร็วเชิงมุมเป็น ในช่วงเวลานั้นความเร่งเชิงมุมคงที่เท่ากับ จะได้สมการการเคลื่อนที่แบบหมุน เมื่อพิจารณาขนาดของปริมาณต่าง ๆ จะได้![]() (1)
(1)![]() ...(2)เมื่อพิจารณาการกระจัดเชิงมุม โดยใช้ความเร็วเชิงมุมเฉลี่ย
...(2)เมื่อพิจารณาการกระจัดเชิงมุม โดยใช้ความเร็วเชิงมุมเฉลี่ย![]() ...(3)เมื่อนำ t จาก (1) แทนใน (3) จะได้
...(3)เมื่อนำ t จาก (1) แทนใน (3) จะได้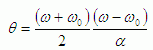
![]()
![]() ...(4)เมื่อนำ จากสมการ (2) แทนใน (4) จะได้
...(4)เมื่อนำ จากสมการ (2) แทนใน (4) จะได้![]()
![]() สมการสำหรับการเคลื่อนที่แบบหมุนที่มีแกนหมุนคงที่มีรูปแบบคล้ายกันมากกับสมการการเคลื่อนที่ในแนวเส้นตรงที่มีความเร่งคงที่ เมื่อเปรียบเทียบกัน จะได้ดังนี้
สมการสำหรับการเคลื่อนที่แบบหมุนที่มีแกนหมุนคงที่มีรูปแบบคล้ายกันมากกับสมการการเคลื่อนที่ในแนวเส้นตรงที่มีความเร่งคงที่ เมื่อเปรียบเทียบกัน จะได้ดังนี้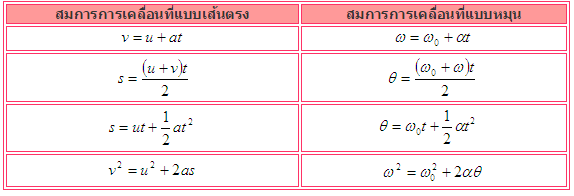
กลับไปที่เนื้อหา
โมเมนต์ความเฉื่อย (I)

ลองนึกภาพกำลังหมุนล้อ ถ้าเป็นล้อเบา ๆ เช่น จักรยาน จะรู้สึกว่าออกแรงหมุนได้ง่าย แต่ถ้าเปลี่ยนจากล้อจักรยานมาเป็นล้อของรถสิบล้อ จะรู้สึกว่ามันหมุนยาก ความยากง่ายในการหมุนนี้เกิดจากโมเมนต์ความเฉื่อย I ถ้าโมเมนต์ความเฉื่อยยิ่งมาก ก็จะยิ่งหมุนได้ยากขึ้นนั่นเอง
ในกรณีที่จุดมวล สูตรหาโมเมนต์ความเฉื่อยคือ
I=mr2
โดย m คือมวล และ r คือระยะจากแกนหมุน
นอกจากนี้ถ้ามีจุดมวลหลายก้อนรอบแกน จะได้สูตรคือ
I = ∑ (miri2)
จะสังเกตว่า วัตถุที่มีมวลเท่ากันไม่จำเป็นต้องมีโมเมนต์ความเฉื่อยเท่ากัน เพราะระยะจากแกนหมุนอาจต่างกัน
ในกรณีที่เป็นมวลก้อนใหญ่หรือวัตถุแข็งเกร็งเช่น ทรงกลม วงแหวน แผ่นจานแบน ก็จะหาโมเมนต์ความเฉื่อยได้จากการจินตนาการว่าก้อนวัตถุเกิดจากจุดมวลหลายจุดรวมกัน แต่การคำนวณต้องใช้คณิตศาสตร์ระดับสูง ดังนี้
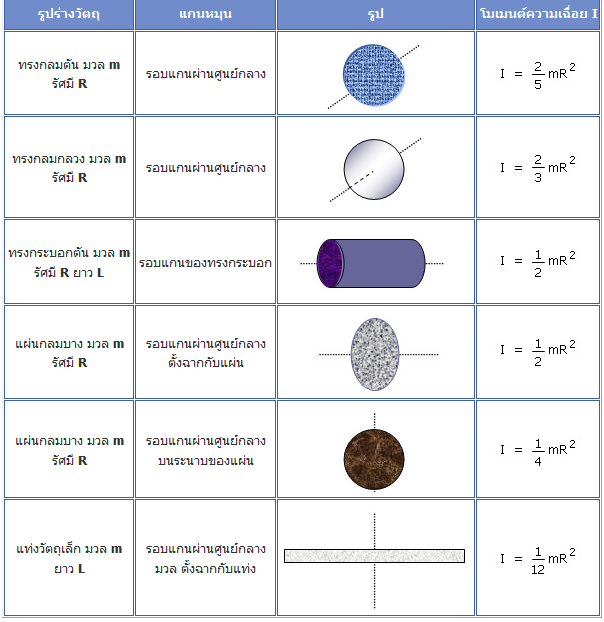
ในเรื่องการหมุน เราสามารถกำหนดแกนหมุนได้หลายแกน ดังนั้นต้องกำหนดให้ได้ก่อนว่า มันหมุนรอบแกนไหน เพราะปริมาณทางฟิสิกส์ เช่น โมเมนต์ ความเฉื่อยและทอร์กนั้นขึ้นอยู่กับตำแหน่งของแกนหมุน
ทฤษฎีแกนขนาน
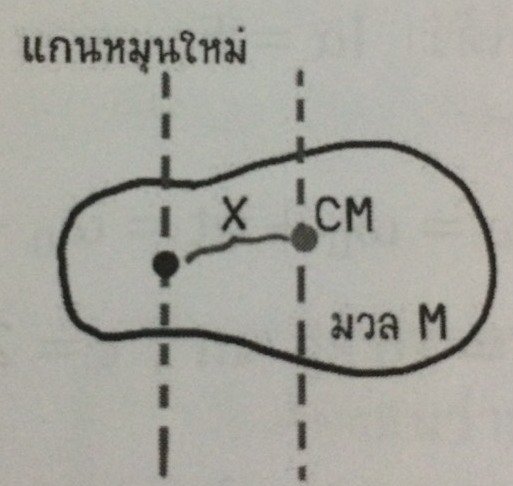
เป็นทฤษฎีสำหรับช่วยหาโมเมนต์ความเฉื่อย สมมติก้อนวัตถุ M กำลังเคลื่อนหมุนรอบจุด CM ด้วยโมเมนต์ความเฉื่อย ICMจากนั้นเราจะเลื่อนแกนหมุนไปให้ห่างจาก จุด CM เป็นระยะ x จะได้ว่า Inew= ICM+ Mx2
กลับไปที่เนื้อหา
การกลิ้งแบบไม่ไถล
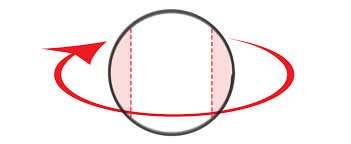
เมื่อเราออกแรงกระทำกับวัตถุ จะเกิดการเคลื่อนที่สองแบบซึ่งเป็นอิสระต่อกัน คือการเลื่อนตำแหน่งแนวตรง และการหมุนรอบจุดศูนย์กลางมวล (CM) ของก้อนวัตถุ
1. การเลื่อนตำแหน่งแนวตรง
จะเกิดขึ้นเสมอเมื่อมีแรงกระทำกับวัตถุ คือการที่วัตถุทั้งก้อนเกาะไปด้วยกัน และเคลื่อนที่ไปในทิศทางเดียวกันทั้งหมดด้วยอัตราเร็ว v เท่ากัน ถ้าวัตถุเคลื่อนที่แบบเลื่อนตำแหน่งเพียงอย่างเดียวก็จะเหมือนกับการเคลื่อนที่ทั่วไป คือทั้งก้อนวัตถุเคลื่อนที่ไปด้วยกัน
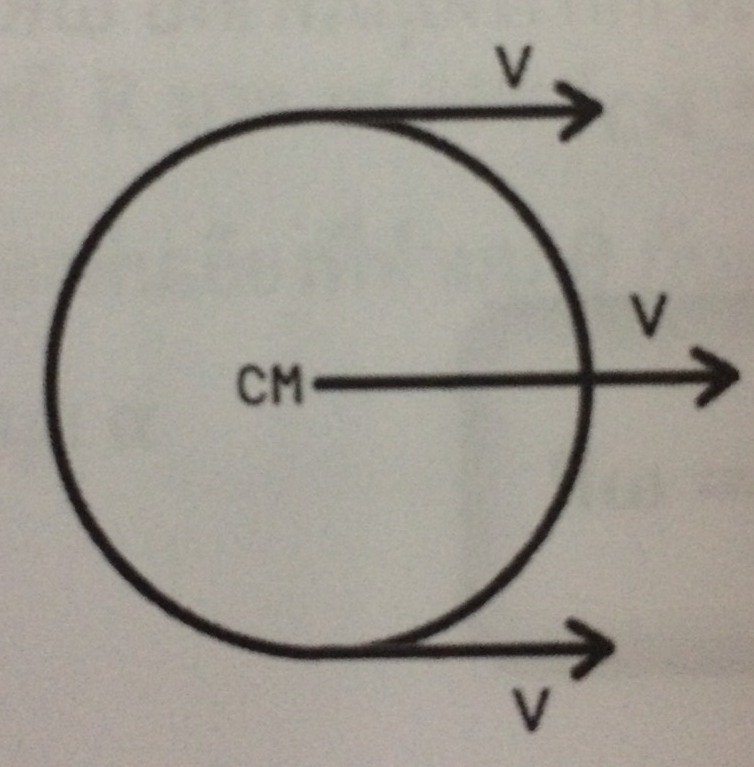
2. การหมุนรอบจุดศูนย์กลางมวล
จะเกิดขึ้นเมื่อทอร์กรอบจุด CM ไม่เป็นศูนย์ (แนวแรงไม่ผ่านจุด CM) คือการที่วัตถุแต่ละจุดหมุนรอบ CM ด้วยอัตราเร็วเชิงมุม ω เท่ากัน ถ้าวัตถุเคลื่อนที่แบบหมุนเพียงอย่างเดียว (ไม่เลื่อนตำแหน่ง) ก็จะเห็นวัตถุอยู่กับที่ แต่หมุนรอบจุด CM ของตัวเองไปเรื่อย ๆ ทั้งนี้ถ้าเราเลือกจุดมวลที่สนใจมาจุดหนึ่ง เราสามารถมองการหมุนเป็นการเคลื่อนที่แนวงกลมรอบแกนหมุนได้ โดยอัตราเร็วของจุดวัตถุจะมีค่าเป็น v= ωr และมีทิศตามแนวการหมุนของจุดมวลในขณะนั้น ซึ่งจุดมวลแต่ละจุดจะมีระยะ t จาก CM ไม่เท่ากัน จึงทำให้ v ต่างกัน
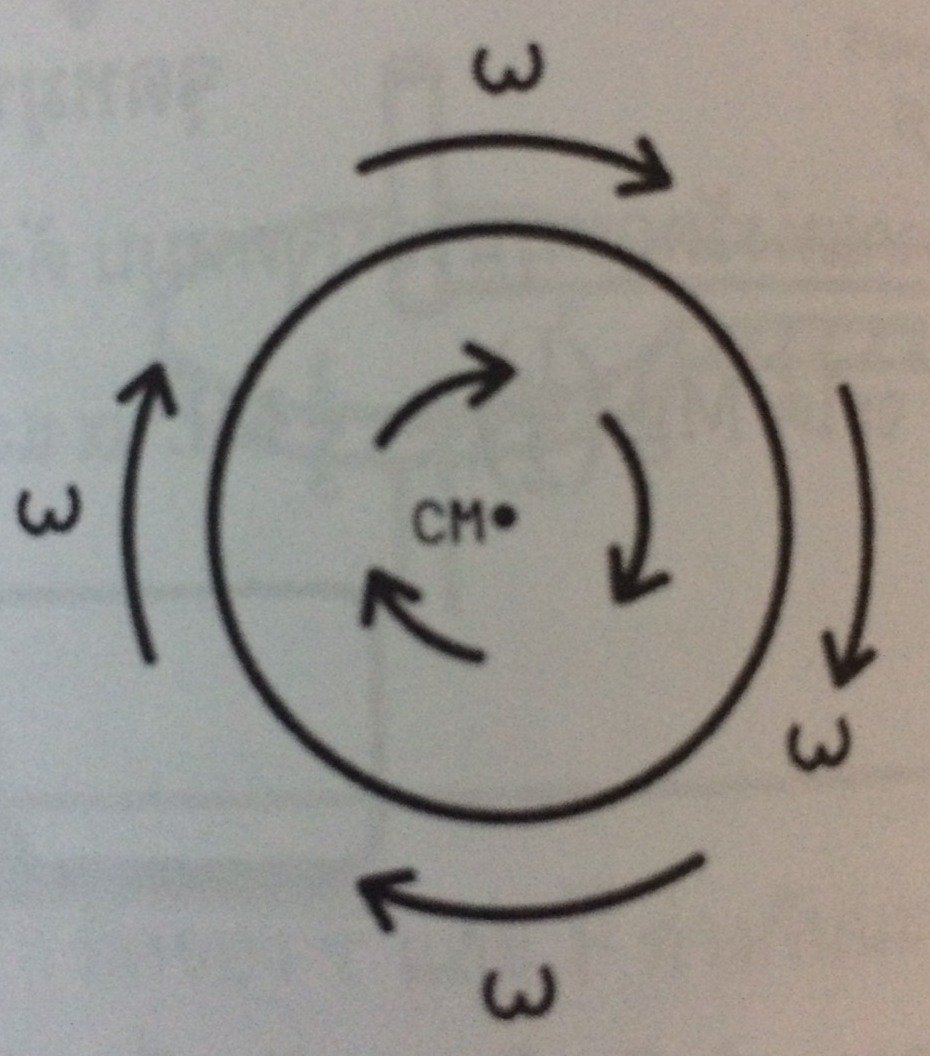
วัตถุสามารถเลื่อนตำแหน่งอย่างเดียวก็ได้ หรือจะหมุนอย่างเดียวก็ได้ หรือจะเคลื่อนที่ทั้งแบบเลื่อนตำแหน่งและแบบบหมุนไปพร้อมๆกันก็ได้ ถ้าวัตถุมีทั้งการเลื่อนตำแหน่งและการหมุน ก็จะเรียกว่าการกลิ้ง ซึ่งออกมาในลักษณะที่ว่า จุด CM จะเลื่อนไปเรื่อย ๆ ด้วยอัตราเร็ว v และจุดที่อยู่รอบ ๆ ก็จะหมุนรอบจุด CM ไปในขณะเดียวกัน
การกลิ้งแบบไม่ไถล คือการกลิ้งที่ทำให้ความเร็วลัพธ์ตรงจุดสัมผัสพื้นเท่ากับศูนย์ จุดที่วัตถุสัมผัสพื้น จะมีความเร็วจากการเลื่อนตำแหน่งเท่ากับ v ไปทางขวา และความเร็วจากการหมุน เท่ากับ ωR ไปทางซ้าย ความเร็วรวมคือ v-ωR จากเงื่อนไขที่ทำให้เกิดการกลิ้งแบบไม่ไถล ก็คือความเร็วลัพธ์ v-ωR = 0 ดังนั้นเราจะได้ว่า v= ωR
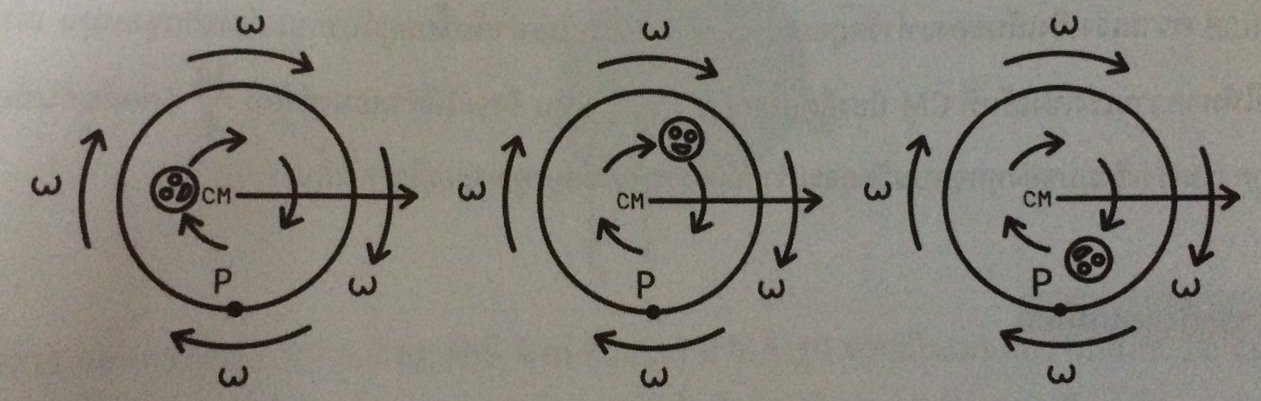
จากความสัมพันธ์ v= ωR เรายังอาจหาความเร็วรวมที่จุดอื่น ๆ ของวัตถุได้ด้วย เช่นที่จุดบนสุดมีความเร็วจากการเลื่อนตำแหน่งเท่ากับ v ไปทางขวา และความเร็วจากการหมุนเท่ากับไป ωR ไปทางขวา ดังนั้น ความเร็วรวมคือ v+ωR=2v ไปทางขวานั่นเอง
กรณีอื่น ๆ
ωR < vCMหรือพูดอีกแบบได้ว่า กลิ้งครบหนึ่งรอบได้ระยะบนพื้นมากกว่า 2¶R เช่น ขับรถเร้วมาก ๆ และเหยียบเบรคทันที จะมีอยู่ช่วงหนึ่งที่ล้อจะไถลไปข้างหน้า ตัวบ้อไถลไปกับพื้น (ช่วงที่ได้ยินเสียงเอี๊ยดอ๊าด)
ωR > vCMหรือพูดอีกแบบได้ว่า กลิ้งครบหนึ่งรอบได้ระยะบนพื้นน้อยกว่า 2¶R เช่น ช่วงเวลาขับรถตกหลุมโคลน และเหยียบคันเร่งเพื่อให้ล้อขึ้นจากหลุม เป็นต้น
อ้างอิง : หนังสือจบกันทีฟิสิกส์
กลับไปที่เนื้อหา



