แม้ว่าคำถามเกี่ยวกับวิธีการในการเอาชนะเกมค้อน กระดาษ กรรไกรจะสร้างความรำคาญใจให้กับนักคณิตศาสตร์และนักทฤษฎีเกมบ้างในบางครั้ง แต่คำถามเหล่านั้นก็ยังคงสร้างความน่าสนใจและจุดประกายให้นักคิดพยายามหาคำตอบในเรื่องของกลยุทธ์ที่ดีที่สุดในการเอาชนะฝ่ายตรงข้ามอยู่ดี

เกมค้อน กระดาษ กรรไกร (Rock–paper–scissors)

          หรือที่เรียกแบบไทยๆ ว่าเกมเปายิ้งฉุบ เป็นเกมชนิดหนึ่งที่นิยมเล่นในเด็กและวัยรุ่นทั่วโลก สำหรับวิธีเล่นเกมนั้นจะอาศัยการแสดงสัญลักษณ์ด้วยมือในการเล่นระหว่างผู้เล่นสองฝ่าย ซึ่งการทำท่าทางด้วยมือมี 3 แบบได้แก่ ค้อน (กำมือ) กรรไกร (ยื่นเฉพาะนิ้วชี้และนิ้วกลาง) และกระดาษ (แบมือ)

ภาพที่ 1 การเล่นเกมค้อน กระดาษ กรรไกร
ที่มา Chris Wang/flickr

ตามการวิเคราะห์ด้วยทฤษฎีเกมแบบคลาสสิก (Classical game theory) กลยุทธ์ที่ดีที่สุดที่ถูกแนะนำในการเล่นเกมเปายิ้งฉุบคือ การเล่นแบบสุ่ม (Random) หมายความว่า ผู้เล่นจะต้องออกค้อน กรรไกร กระดาษโดยไม่ซ้ำกันในแต่ละรอบ เพื่อไม่ให้ฝ่ายตรงข้ามสามารถคาดเดาเกมการเล่นและยังช่วยในการหลีกเลี่ยงการโจมตีจากคู่แข่งอีกด้วย ซึ่งเป็นไปตามลักษณะของสมดุลทางกลยุทธ์ที่เรียกว่าสมดุลของแนช (Nash equilibrium)

ในขณะที่ Zhijian Wang จากมหาวิทยาลัยเจ้อเจียง ประเทศจีน หนึ่งในนักคณิตศาสตร์ที่พยายามหาคำอธิบายถึงวิธีการที่ช่วยเพิ่มโอกาสในการชนะเกมเปายิ้งฉุบนั้นพบวิธีการที่แตกต่าง นอกเหนือจากโอกาสในการแพ้ ชนะหรือเสมอจากการเล่นแบบสุ่ม

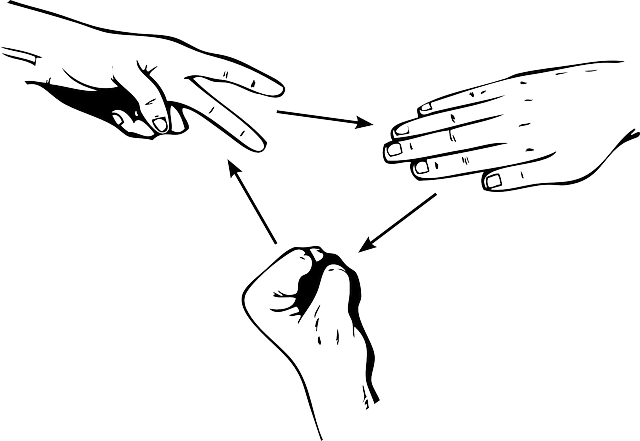
ภาพที่ 2 persistent cyclic flows
ที่มา Open Clipart Vectors/pixabay

สำหรับความพยายามของเขาและทีมงานที่ได้ทำการศึกษาทดลองกับผู้เล่นจริงจำนวน 360 คน โดยการแบ่งกลุ่มของผู้เล่นออกเป็น 12 กลุ่ม และให้ผู้เล่นแต่ละคนเล่นเกมคนละ 300 รอบกับผู้เล่นภายในกลุ่ม โดยมีการให้รางวัลเป็นแรงจูงใจต่อผู้เล่นที่ชนะด้วย จากการทดลองพบว่า ผู้เล่นแต่ละคนมีการเลือกใช้ค้อน กระดาษ และกรรไกรสลับกันไปในการเล่นแบบสุ่มตามการคาดการณ์ไว้ แต่อย่างไรก็ตามจากการสังเกตอย่างใกล้ชิดทำให้ทีมงานพบพฤติกรรมการเล่นที่แตกต่างโดยพบว่า ผู้เล่นที่ชนะมักจะยึดติดกับเกมการชนะของตนเองและทำซ้ำในทางเลือกเดิม ในขณะที่ผู้แพ้มีแนวโน้มที่จะเปลี่ยนกลยุทธ์ในลำดับถัดไป กล่าวคือเป็นกลยุทธ์ในลักษณะของ  "win-stay lose-shift"   ซึ่งจากพฤติกรรมการเล่นเกมข้างต้นเป็นลักษณะการเล่นที่เป็นวงจรแบบหมุนเวียนต่อเนื่องที่เรียกว่า “Persistent cyclic flows”

ในทางปฏิบัติ ผู้เล่น ก และผู้เล่น ข เริ่มต้นการเล่นเกมเปายิ้งฉุบด้วยวิธีการแบบสุ่ม

           หากผู้เล่น ก ออกค้อน ในขณะที่ผู้เล่น ข ออกกรรไกร ในเกมแรกผู้เล่น ข เป็นฝ่ายแพ้  ผู้แพ้สามารถอนุมานได้ว่าผู้ชนะจะยึดติดกับการเล่นเกมแบบเดิมในรอบถัดไป ดังนั้นผู้เล่น ข จึงควรออกกระดาษเพื่อเอาชนะผู้เล่น ก 

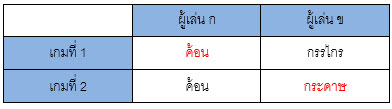
          ในรอบการเล่นหลังจากนั้น หากว่าผู้เล่น ก แพ้ ผู้เล่น ก ก็สามารถคาดการณ์การใช้กลยุทธ์ในแบบเดียวกันนี้ และเลือกใช้กรรไกรเพื่อพลิกกลับมาเอาชนะผู้เล่น ข ได้อีกครั้ง

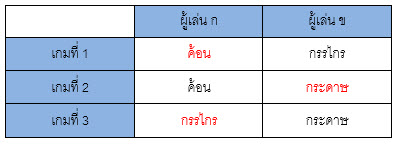
          ทั้งนี้กลยุทธ์แบบ "win-stay lose-shift" ยังเป็นที่รู้จักในทฤษฎีเกมในแง่ของการตอบสนองตามเงื่อนไขที่เรียกว่า conditional response ซึ่งนักวิจัยตั้งสมมติฐานไว้ว่า การตอบสนองดังกล่าวนั้นอาจเป็นกลไกที่หยั่งรากลึกในสมองของมนุษย์ อีกนัยยะหนึ่งคือกลยุทธ์ดังกล่าว เสมือนเป็นจุดตัดระหว่างคณิตศาสตร์และจิตวิทยาในลักษณะของทฤษฎีเกมที่อยู่เบื้องหลังวิธีการที่มนุษย์ตัดสินใจในสถานการณ์การแข่งขัน นั่นจึงเป็นหัวข้อที่ท้าทายอย่างมากสำหรับการศึกษาค้นคว้าในอนาคต

          นอกจากนี้จากสถิติการเล่นเกมเปายิ้งฉุบจากสมาคมเกมค้อน กระดาษ กรรไกรโลก (World Rock Paper Scissor Society) ยังได้มีการเผยแพร่คำแนะนำที่ช่วยเพิ่มโอกาสในการเป็นผู้ชนะในการแข่งขัน ดังนี้

• ผู้ชายมักจะเปิดเกมการเล่นด้วยค้อนเสมอ หากกำลังเล่นเกมนี้กับผู้ชายให้เริ่มต้นเกมด้วยกระดาษ
• กรรไกร เป็นการเปิดเกมการเล่นที่มีสถิติชนะมากที่สุด
• สยบฝ่ายตรงข้ามด้วยความจริง ด้วยการประกาศสิ่งที่จะทำและปฏิบัติตาม เนื่องจากไม่มีใครเชื่อว่าผู้เล่นที่ประกาศสิ่งที่ตนกำลังจะเล่นจะทำตามคำพูดเหล่านั้นจริงๆ

           อย่างไรก็ตาม ใช้ประโยชน์จากข้อมูลข้างต้นอย่างชาญฉลาดและมีสติ กลยุทธ์เหล่านี้อาจช่วยคุณได้ อย่างน้อยที่สุดก็ไม่ต้องรับผิดชอบต่อการล้างจานหรือการขัดห้องน้ำในเย็นวันอาทิตย์

แหล่งที่มา

Bin X, Hai-Jun Z and Zhijian W. Cycle frequency in standard Rock–Paper–Scissors games: Evidence from experimental economics. Sciencedirect.2013; 392, 4997-5005.

HARRISON JACOBS. (2015, 17 December). How to Beat Anyone at Rock-Paper-Scissors, According to a Mathematician.
            Retrieved November 30, 2017, 
            from https://www.sciencealert.com/how-to-beat-anyone-at-rock-paper-scissors-according-to-a-chinese-mathematician

James Morgan. (2014, 2 May). How to win at rock-paper-scissors.
            Retrieved November 30, 2017, 
            from http://www.bbc.com/news/science-environment-27228416

Theresa Locker. (2015, 4 February). Win at Rock-Paper-Scissors Every Time, With Math.
            Retrieved November 30, 2017, 
            from https://motherboard.vice.com/en_us/article/gvym4x/game-theory-rock-paper-scissors

Elizabeth Knowles. (2015, 24 December). How to Win at Rock-Paper-Scissors, According to Math.
            Retrieved November 30, 2017, 
            from http://thescienceexplorer.com/universe/how-win-rock-paper-scissors-according-math

Zhijian W, Bin X and Hai-Jun Z. (2014, 25 July). Social cycling and conditional responses in the Rock-Paper-Scissors game
            Retrieved November 30, 2017, 
            from https://www.nature.com/articles/srep05830.pdf