ฟังก์ชันและฟังก์ชันในคอมพิวเตอร์
ฟังก์ชัน
ฟังก์ชันเป็นวัตถุเชิงคณิตศาสตร์ที่ถูกนำไปประยุกต์ใช้ในศาสตร์ต่างมากมายไม่ว่าจะเป็นวิทยาศาสตร์กายภาพและชีวภาพ วิศวกรรม และเศรษฐศาสตร์ คำแปลของฟังก์ชันคือการทำงาน นั้นหมายความว่าหากเราต้องการอธิบายการทำงานของสิ่งต่าง ๆเราสามารถใช้ฟังก์ชันเป็นตัวแทนเมื่ออธิบายการทำงานนั้น ๆได้ ในทางวิทยาศาสตร์กายภาพชีวภาพ เราใช้ฟังก์ชันอธิบายการทำงานหรือพฤติกรรมของระบบในธรรมชาติเช่นพฤติกรรมคงที่ พฤติกรรมการลดลงหรือเพิ่มขึ้นอย่างเป็นสัดส่วนสามารถอธิบายผ่านฟังก์ชันเชิงเส้น แต่หากพฤติกรรมมีการเพิ่มขึ้นในช่วงแรกอย่างช้า ๆแต่จะเพิ่มขึ้นอย่างรวดเร็วเมื่อผ่านไปช่วงเวลาหนึ่ง หรือมีการลดลงอย่างรวดเร็วในช่วงแรกแต่จะค่อยลดลงอย่างช้าเมื่อเวลาผ่านไปพฤติกรรมที่กล่าวมาอธิบายได้ด้วยฟังก์ชันเอกซ์โปเนนเชียล นอกจากนี้หากระบบมีการกวัดแกว่งเราสามารถอธิบายได้ด้วยฟังก์ชันไซน์หรือโคไซน์เป็นต้น
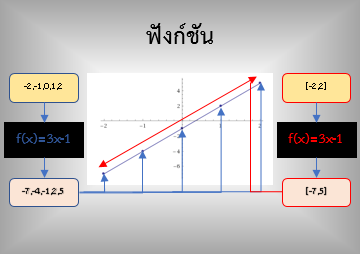
ภาพฟังก์ชันที่มีโดเมนเต็มหน่วยและโดเมนต่อเนื่อง
ที่มา วีระ ยุคุณธร
ฟังก์ชันและนิยามของฟังก์ชัน
ในการทำงานของระบบจะต้องมีสิ่งที่นำเข้าเรียกว่าอินพุตและผลการทำงานที่ออกจากระบบเรียกว่าเอาต์พุต การทำงานแบบฟังก์ชันนั้นมีเงื่อนไขอยู่ว่า อินพุต 1 ค่าจะต้องให้เอาท์พุตเพียงค่าเดียว กล่าวคือ 1 คำสั่งจะให้ผลลัพธ์เพียงแค่ผลลัพธ์เดียว สมมติให้ฟังก์ชัน f มีอินพุต i1 ทำให้เกิดเอาท์พุต o1 เราเขียนความสัมพันธ์ได้ในรูปคู่อันดับ ( i1,o1 ) แต่ถ้าหากอินพุต i1 ทำให้เกิดเอาท์พุต o2 ด้วยนั้นคือ ( i1,o2 ) นั้นคือ f = { ( i1,o1 ), ( i1,o2 ) } ลักษณะดังกล่าวไม่เป็นฟังก์ชัน เราสามารถให้นิยามได้ดังนี้
นิยาม สมมติให้ ( x,y ) และ ( x,z ) เป็นคู่อันดับใด ๆในฟังก์ชันแล้ว y = z
ข้อสังเกต f = { ( i1,o1 ), ( i2,o1 ) } ถือว่าเป็นฟังก์ชันเนื่องจาก 1 อินพุตทำให้เกิด 1 เอาท์พุต จึงไม่ขัดแย้งกับนิยามที่กำหนดไว้ สังเกตได้ว่าความสัมพันธ์ที่เป็นฟังก์ชันนั้นอาจเป็นความสัมพันธ์แบบ one to one หรือ many to one ก็ได้
อย่างไรก็ตามฟังก์ชันสำหรับคอมพิวเตอร์กับฟังก์ชันที่ใช้อธิบายระบบในธรรมชาติอาจมีความแตกต่างกัน เนื่องจากระบบการทำงานของคอมพิวเตอร์ส่วนใหญ่เป็นระบบเต็มหน่วยไม่ว่าจะเป็นการจัดการฐานข้อมูล การเข้ารหัสและถอดรหัส ในขณะที่ฟังก์ชันที่ใช้อธิบายระบบในธรรมชาตินั้นเป็นระบบชนิดต่อเนื่องนั้นเพราะว่าตัวแปรต้นในธรรมชาติมักมีลักษณะต่อเนื่องเป็นเนื้อเดียวกันสิ่งที่ทำให้เกิดความแตกต่างนี้คือโดเมนของฟังก์ชัน
โดเมนและเรนจ์
โดเมนคือเซตของอินพุตที่ป้อนเข้าสู่ระบบการทำงาน กำหนดโดเมน D1 และ D2 ดังนี้
D1 = { -2, -1, 0, 1, 2 } และ D2 = (-2,2) := เซตของจำนวนจริงระหว่าง -2 และ 2
ถ้าเรากำหนด input -----> f -----> output โดยที่ f(input) = 3 x input – 1
พิจารณา D1 จะเห็นว่า
(-2) -----> f(-2) = 3 x (-2) – 1 -----> -7
(-1) -----> f(-1) = 3 x (-1) – 1 -----> -4
0 -----> f(0) = 3 x (0) – 1 -----> -1
1 -----> f(1) = 3 x (1) – 1 -----> 2
2 -----> f(2) = 3 x (2) – 1 -----> 5
เราจะได้เซตของเอาท์พุตเรียกว่า เรนจ์ R1 = { -7, -4, -1, 2, 5 }
พิจารณา D2 จะเห็นว่า input สมมติแทนด้วยตัวแปร a จะได้ว่า -2 < a < 2
a -----> f(a) = 3 x (a) – 1 -----> 3a - 1
จะเห็นได้ว่า 3(-2) - 1< 3a - 1 < 3(2) - 1 พบว่าเรนจ์ของฟังก์ชันคือ R2 = ( -7,5 )
เราเขียนฟังก์ชันการทำงานได้ดังนี้ f : D1 -----> R1 และ f : D2 -----> R2 ตามลำดับ จากตัวอย่างข้างต้นหากเรากำหนดอินพุตเป็น (D1) แต่ต้องการคำนวณ f(3) เมื่อพิจารณาการทำงานฟังก์ชันเขียนแบบแจงสมาชิกได้ดังนี้ f = { (-2,-7), (-1,-4), (0,-1), (1,2), (2,5) } จะเห็นว่าอินพุต 3 ไม่อยู่ในระบบการทำงานทำให้ฟังก์ชันไม่สามารถทำงานได้ นอกจากนี้ถ้าเรากำหนด g (x) = 1/x โดยที่โดเมนของ g แทนด้วย Dg = { -1, 0, 1 } จะเห็นว่าฟังก์ชันคำนวณค่า -1 ได้ แต่เมื่อ input = 0 ฟังก์ชัน g(0) = 1/0 ไม่นิยามหากเราทำการโปรแกรมเมื่อถึงค่า 0 โปรแกรมจะเกิด error และหยุดการทำงานได้ ดังนั้นการสร้างหรือกำหนดฟังก์ชันให้ทำงานได้มีความจำเป็นที่จะต้องตรวจสอบ โดเมน เรนจ์ และความเป็นฟังก์ชัน
ฟังก์ชันที่ถูกนิยามไว้ดีแล้ว
สำหรับฟังก์ชันที่ได้ตรวจสอบโดเมน เรนจ์ และความเป็นฟังก์ชันอย่างรัดกุม จนสามารถทำงานได้แบบไม่มีข้อผิดพลาดสิ่งที่ต้องตรวจสอบมีดังนี้
- โดเมนของฟังก์ชันที่ซึ่งทุกสมาชิกในโดเมนจะต้องสามารถหาค่าฟังก์ชันได้
- เรนจ์ของฟังก์ชันจะต้องครอบคลุมเอาต์พุตจากการทำงาน
- การทำงานเป็นฟังก์ชัน
หากผ่านการตรวจสอบทั้ง 3 ข้อข้างต้นถือว่าฟังก์ชันดังกล่าวเป็นฟังก์ชันที่ถูกนิยามไว้ดีแล้ว (well-defined)
ตัวอย่างเช่นกำหนดโดเมน (Df) เป็นจำนวนจริง เรนจ์ (Rf) เป็นจำนวนจริง และฟังก์ชัน f (x) = ( x – 1 )1/2 จะเห็นได้ว่าการสร้างฟังก์ชันดังกล่าวทำให้เกิดข้อผิดพลาดในการทำงานเนื่องจากฟังก์ชันมีสัญลักษณ์กรณฑ์แต่โดเมนและเรนจ์เป็นจำนวนจริงใด ๆซึ่งขัดแย้งกับนิยามของกรณฑ์ที่ว่า ค่าที่อยู่ในเครื่องหมายกรณฑ์จะต้องมีค่ามากกว่าหรือเท่ากับศูนย์ นั้นคือ x -1 จะต้องมีค่ามากกว่าหรือเท่ากับศูนย์ หากค่าภายในกรณฑ์มีค่าเป็นลบแล้วจะทำให้เกิดจำนวนเชิงซ้อน เพื่อให้ฟังก์ชันสามารถทำงานได้เราสามารถแก้ไขขึ้นกับความเหมาะสมและความต้องการใช้งานในที่จะนำเสนอ 2 แนวทางดังนี้
แนวทางที่ 1 แก้ไขโดเมนโดยที่เอาท์พุตยังคงเป็นจำนวนจริงนั้นคือ กำหนดโดเมนฟังก์ชันใหม่โดยเลือกเฉพาะ x ที่ทำให้ x – 1 มีค่ามากกว่าหรือเท่ากับศูนย์นั้นคือ Df = [1,infinity)
แนวทางที่ 2 แก้ไขเรนจ์โดยขยายเซตที่ครอบคลุมเอาท์พุตนั้นคือ Rf := เซตของจำนวนเชิงซ้อน เป็นต้น
แหล่งที่มา
Skvarcius R., Robinson W.B. (1986). Discrete mathematics with computer science applications. The Benjamin/Cummings Publishing Company.
กลับไปที่เนื้อหา
ฟังก์ชัน 1-1 และ ฟังก์ชันทั่วถึง
ในหัวข้อก่อนหน้านี้เราได้ศึกษาเกี่ยวกับการสร้างฟังก์ชันเพื่อให้ฟังก์ชันสามารถทำงานได้หรือถูกนิยามไว้ดีแล้วในหัวข้อนี้เราจะศึกษาการสร้างฟังก์ชันให้มีประสิทธิภาพและมีความเหมาะสมโดยเราจะคำนึงถึงเรนจ์ของฟังก์ชันเป็นหลักเนื่องจากในงานประยุกต์สิ่งที่เราต้องการหรือเป้าหมายของการออกแบบการทำงานคือผลลัพธ์หรือเอาท์พุต
ความสัมพันธ์ที่เป็นฟังก์ชันนั้นประกอบด้วยความสัมพันธ์แบบ one to one และ many to one สมมติให้การทำงานต้องการให้เกิดเอาท์พุต o1 ซึ่งเมื่อพิจารณาพบว่าอินพุต i1 และ i2 ทำให้เกิดเอาท์พุต o1 ถ้าเป้าหมายเราต้องการ o1 การเลือกสมาชิกในเซตของอินพุตหรือโดเมนนั้นอาจเลือก i1 หรือ i2 อย่างใดอย่างหนึ่งก็เพียงพอสำหรับการได้มาซึ่ง o1 เราเรียกฟังก์ชันการทำงานแบบนี้ว่าฟังก์ชันหนึ่งต่อหนึ่ง (หนึ่งต่อหนึ่ง) ในทางกลับกันการสร้างฟังก์ชันให้ทำงานได้เรนจ์ของฟังก์ชันถูกสร้างให้ครอบคลุมเอาท์พุตที่เกิดขึ้นก็เพียงพอแต่หากเราต้องการกำหนดทรัพยากรให้เหมาะสมเราควรกำหนดเรนจ์ของฟังก์ชันให้เป็นเซตที่บรรจุเฉพาะเอาท์พุตที่เกิดจากโดเมนเท่านั้นเกิดเป็นแนวคิดของฟังก์ชันทั่วถึง
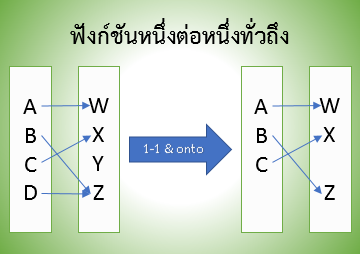
ภาพการแปลงฟังก์ชันทั่วไปให้เป็นฟังก์ชันหนึ่งต่อหนึ่งทั่วถึง
ที่มา วีระ ยุคุณธร
ฟังก์ชันหนึ่งต่อหนึ่ง
ดังที่กล่าวมาในข้างต้นว่าฟังก์ชันการทำงาน f = { ( i1,o1 ), ( i2,o1 ) } มีโดเมน = { i1, i2 } และมีเรนจ์ = { o1 } ซึ่งเป็นการทำงานที่ซ้ำซ้อนหากเราต้องการเอาท์พุต o1 เราควรเลือกอินพุต i1 หรือ i2 อย่างใดอย่างหนึ่งก็เพียงพอนั้นคือฟังก์ชัน { ( i1,o1 ) } ให้ผลลัพธ์แบบเดียวกันกับ { ( i1,o1 ), ( i2,o1 ) } สรุปได้ว่าฟังก์ชันหนึ่งต่อหนึ่งนั้นเอาท์พุตของฟังก์ชันมาจากอินพุตเพียงค่าเดียวให้นิยามเชิงคณิตศาสตร์ได้ดังนี้
นิยาม ถ้า ( x,z ) และ ( y,z ) เป็นสมาชิกของฟังก์ชันหนึ่งต่อหนึ่ง แล้ว x = y หรือกล่าวได้ว่า ถ้า f เป็นฟังก์ชันหนึ่งต่อหนึ่ง และ f(x) = f(y) แล้ว x = y
ตัวอย่างฟังก์ชันหนึ่งต่อหนึ่ง กำหนดให้ f(x) = 3x – 1 สมมติให้ f(x) = f(y) เป็นจริงจะต้องแสดงให้ได้ว่า x = y เป็นจริงเช่นเดียวกัน พิจารณา 3x – 1 = 3y -1 จะเห็นได้โดยง่ายว่า x = y ดังนั้น f เป็นฟังก์ชันหนึ่งต่อหนึ่ง
ตัวอย่างฟังก์ชันที่ไม่ใช้ฟังก์ชันหนึ่งต่อหนึ่ง กำหนดให้ f(x) = x2 พิจารณากฎตรรกศาสตร์ให้
p -> q เป็นเท็จ สมมูลกับ นิเสธของ p -> q เป็นจริง
สมมูลกับ นิเสธ ของ นิเสธ p หรือ q เป็นจริง
สมมูลกับ p และ นิเสธ q เป็นจริง
เราจะต้องแสดงว่า p เป็นจริง และ นิเสธ q เป็นจริง จากการให้นิเสธ q เป็นจริงนั้นคือให้เลือก x ไม่เท่ากับ y แต่ f(x) = f(y) ในที่นี้เราเลือก x = 2 และ y = -2 เห็นได้โดยง่ายว่า x ไม่เท่ากับ y แต่ f(x) = f(y) เลือก x = 2 และ y = -2 จะได้ว่า f(x) = 22 = 4 = -22 = f(y) ดังนั้น f ไม่เป็นฟังก์ชันหนึ่งต่อหนึ่ง
ฟังก์ชันทั่วถึง
การสร้างเรนจ์ของฟังก์ชันโดยเลือกบรรจุเฉพาะเอาท์พุตที่เกิดจากโดเมนเท่านั้น และไม่มีเอาท์พุตใดที่ไม่ใช้ผลลัพธ์ของการทำงานหรือค่าฟังก์ชัน สังเกตว่าหากเราเลือกสมาชิกในเรนจ์ของฟังก์ชันตัวใด ๆมา เราจะต้องสามารถระบุอินพุตที่ทำให้เกิดเอาท์พุตได้ซึ่งให้นิยามเชิงคณิตศาสตร์ได้ดังนี้
นิยาม เราจะกล่าวว่า f เป็นฟังก์ชันทั่วถึงถ้า สำหรับ y ซึ่งเป็นสมาชิกใดๆ ในเรนจ์ของฟังก์ชัน (Rf) จะมี x ซึ่งเป็นสมาชิกในโดเมนของฟังก์ชันที่ซึ่ง y = f(x)
ตัวอย่างฟังก์ชันทั่วถึง ให้ f เป็นฟังก์ชันที่มีโดเมนเป็นจำนวนเต็มและเรนจ์เป็นจำนวนเต็มบวก กำหนดโดย f(x) = |x| จะเห็นว่าไม่ว่าจำนวนเต็มบวก a ใดที่เป็นเรนจ์ของฟังก์ชัน a = |x| เราสามารถหาค่า x ได้นั้นคือ x = a หรือ x = -a ซึ่งเป็นจำนวนเต็มและเป็นสมาชิกในโดเมนของฟังก์ชัน ดังนั้น f จึงเป็นฟังก์ชันทั่วถึง
ตัวอย่างฟังก์ชันที่ไม่เป็นฟังก์ชันทั่วถึง กำหนดให้ f เป็นฟังก์ชันที่มีโดเมนเป็นจำนวนเต็มบวกและมีเรนจ์เป็นจำนวนเต็มบวกซึ่ง f(x) = 3x จะเห็นว่า 1 เป็นจำนวนเต็มบวกและเป็นเรนจ์ของฟังก์ชัน แต่ไม่มีจำนวนเต็มบวก x ใดๆ ที่ทำให้ 3x = 1 ดังนั้น f ไม่เป็นฟังก์ชันทั่วถึง
ฟังก์ชันหนึ่งต่อหนึ่งและทั่วถึง
หมายถึงฟังก์ชันที่เป็นฟังก์ชันหนึ่งต่อหนึ่งและเป็นฟังก์ชันทั่วถึง เมื่อพิจารณาการส่งจะเห็นว่าสมาชิกทุกตัวในโดเมนจะถูกส่งไปเป็นสมาชิกแต่ละตัวในเรนจ์และสมนัยเพียงตัวเดียว ในทางกลับกันจะเห็นว่าเราสามารถทำการส่งจากเรนจ์ของฟังก์ชันกับไปยังโดเมนได้ซึ่งสมาชิกตัวในเรนจ์จะถูกส่งไปยังโดเมนแต่ละตัวที่สมนัยกับสมาชิกในเรนจ์เพียงตัวเดียว การส่งกลับนี้รักษาสมบัติการถูกกำหนดไว้ดีแล้วของฟังก์ชันอีกด้วยเราเรียกการส่งกลับนี้ว่าฟังก์ชันผกผัน
ข้อดีของการออกแบบการทำงานหรือฟังก์ชันที่เป็นหนึ่งต่อหนึ่งและทั่วถึงคือระบบใดก็ตามที่มีลักษณะการทำงานแบบหนึ่งต่อหนึ่งและทั่วถึงระบบนั้นเราสามารถทำการตรวจสอบหรือยืนยันได้ว่าผลลัพธ์หรือเอาท์พุตที่เกิดขึ้นมานี้ได้มากจากอินพุตใด นอกจากจะเป็นการลดความซ้ำซ้อนของการทำงานและการให้ทรัพยากรที่สิ้นเปลืองแล้วยังสามารถตรวจสอบย้อนกลับได้อีกด้วย กรณีที่โดเมนกับเรนจ์เป็นเซตนับได้เรามีทฤษฎีสำหรับการตรวจสอบดังนี้
ทฤษฎีบท กำหนดให้ D และ R เป็นเซตนับได้ทั้งคู่ซึ่งเป็นโดเมนและเรนจ์ของฟังก์ชัน f ตามลำดับ
T1 ถ้า f เป็นฟังก์ชันหนึ่งต่อหนึ่งแล้ว n(D) น้อยกว่าหรือเท่ากับ n(R)
T2 f เป็นฟังก์ชันหนึ่งต่อหนึ่งก็ต่อเมื่อ n(f(A)) น้อยกว่าหรือเท่ากับ n(A)
T3 ถ้า f เป็นฟังก์ชันทั่วถึงแล้ว n(A) มากกว่าหรือเท่ากับ n(B)
T4 ถ้า f เป็นฟังก์ชันหนึ่งต่อหนึ่งทั่วถึงแล้ว n(A) เท่ากับ n(B)
หมายเหตุ การตรวจสอบด้วยทฤษฎีจะต้องใช้บทแย้งสลับที่ทางตรรกศาสตร์เป็นส่วนใหญ่
แหล่งที่มา
Skvarcius R., Robinson W.B. (1986). Discrete mathematics with computer science applications. The Benjamin/Cummings Publishing Company.
กลับไปที่เนื้อหา
ฟังก์ชันในคอมพิวเตอร์
ภาษาโปรแกรมสมัยใหม่จะถูกจัดสรรทรัพยากรในการใช้งานเพื่อการคำนวณและการจัดการข้อมูลไว้มากแต่โดยทั่วไปแล้วมักเป็นฟังก์ชันพื้นฐานที่ถูกใช้อาทิฟังก์ชันตรีโกณมิติ เอกโพเนนเชียล ลอการิทึม และพหุนามเป็นต้นแต่อย่างไรก็ตามหากเราต้องการออกแบบการทำงานหรือการคำนวณที่นอกเหนือจากชุดคำสั่งสำเร็จรูปที่อยู่ในภาษาต่างแล้ว เราสามารถทำการสร้างฟังก์ชันใหม่ได้ในบทเรียนนี้จะศึกษาถึงการสร้างฟังก์ชันคณิตศาสตร์ในภาษาไพทอนซึ่งเป็นภาษาที่เป็นที่นิยมในยุคปัจจุบัน
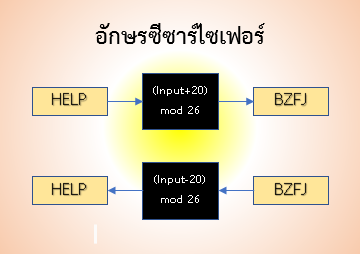
ภาพอักษรซีซาร์ไซเฟอร์
ที่มา วีระ ยุคุณธร
ฟังก์ชันกับโปรแกรมคอมพิวเตอร์
การโปรแกรมคอมพิวเตอร์เป็นการสั่งคอมพิวเตอร์ให้ทำงานเพื่อตอบวัตถุประสงค์ของผู้ใช้ รูปแบบการทำงานที่มีขั้นตอน รูปแบบเป็นแบบเดียวเราจะสร้างฟังก์ชันขึ้นมาสั่งการทำงานคอมพิวเตอร์อาจอยู่ในรูปของโปรแกรมย่อยแต่จะให้ค่าเพียงแค่ค่าเดียว ตัวอย่างโค๊ดการกำหนดฟังก์ชัน
1 def ชื่อฟังก์ชัน(ตัวแปร)
2 # นิยาม
3 return value
บรรทัดที่ 1 ในการสร้างฟังก์ชันใหม่เราจะต้องตั้งชื่อฟังก์ชันในส่วนของ function_name และทำการระบุตัวแปรต้นที่เป็นสมาชิกของโดเมนของฟังก์ชันใน args
บรรทัดที่ 2 การนิยามฟังก์ชันหรือการทำงาน
บรรทัดที่ 3 การส่งค่ากลับอาจมีหรือไม่มีก็ได้
ตัวอย่างเช่นเราต้องการสร้างฟังก์ชันเพื่อหาพื้นที่สี่เหลี่ยมคางหมู
ขั้นตอนที่ 1 เราต้องทำการสร้างฟังก์ชันเชิงคณิตศาสตร์เสียก่อนโดยกำหนดให้ A เป็นฟังก์ชันการคำนวณพื้นที่สี่เหลี่ยมคางหมู ต่อมาเราต้องทราบอินพุต หรือ ตัวแปรซึ่งเป็นพารามิเตอร์ที่ใช้ในการคำนวณพื้นที่ในที่นี้ประกอบมี 3 ตัวแปรได้แก่ ความยาวด้านคู่ขนานสองด้าน และ ความสูง แทนด้วย p1,p2,h ตามลำดับ ณ ขั้นตอนนี้เทียบเท่ากับบรรทัดแรกของโปรแกรม
1 def ชื่อฟังก์ชัน(ตัวแปร) ===> def traparea(p1,p2,h) ===> A(p1,p2,h)
ขั้นตอนที่ 2 เราจะต้องระบุขั้นตอนการทำงานหรือนิยามในที่นี้คือการหาพื้นที่สี่เหลี่ยมคางหมูจากความยาวด้านคู่ขนานสองด้านและความสูงมีสูตรว่าพื้นที่สี่เหลี่ยมคางหมู = 1/2 x ผลบวกด้านคู่ขนาน x สูง
2 นิยาม ===> A = 0.5*(p1+p2)*h
ในที่นี้หากเราให้คำสั่ง traparea(6,4,7) ซึ่งตรงกับสัญลักษณ์คณิตศาสตร์คือ
A(6,4,7) = 0.5*(6+4)*7 =35
โค๊ดฟังก์ชันเพื่อหาพื้นที่สี่เหลี่ยมคางหมู
def traparea(p1,p2,h)
A = 0.5*(p1+p2)*h
แต่สำหรับโปรแกรมไพทอนมีฟังก์ชัน Lambda expressions ซึ่งช่วยให้การสร้างฟังก์ชันเพื่อการคำนวณเชิงคณิตศาสตร์มีความสะดวกมากขึ้นมีโค๊ดกระชับดังนี้
สัญลักษณ์ = lambda กลุ่มตัวแปร : นิยาม
หากนำมาใช้ในการหาสูตรพื้นที่สี่เหลี่ยมคางหมูจะได้
A = lambda p1, p2, h: 0.5*(p1+p2)*h
ซึ่งสามารถเรียกใช้งานแบบฟังก์ชันคณิตศาสตร์ได้คือ A(6,4,7)
ฟังก์ชันในงานทางด้านคอมพิวเตอร์
ฟังก์ชันหนึ่งที่มีบทบาทสำคัญในยุค 4.0 หรือยุคดิจิตอลคือฟังก์ชันแฮชซึ่งเกี่ยวข้องกับระบบความปลอดภัยเป็นฟังก์ชันที่ไม่สามารถหาอินเวอร์ได้ ระบบความปลอดภัยทางคอมพิวเตอร์ส่วนใหญ่จะเกี่ยวข้องกับจำนวนเต็มโดยเฉพาะอย่างยิ่งจำนวนเฉพาะ โดยมีฟังก์ชันเศษตกค้างเป็นฟังก์ชันที่ถูกใช้อย่างมากในงานด้านความปลอดภัยทางคอมพิวเตอร์ ในที่นี้ผู้เขียนจะกล่าวถึงการประยุกต์ใช้ฟังก์ชันเศษตกค้างอย่างง่ายในการส่งข้อความรหัสลับ
กำหนดให้ C เป็นค่าตัวเลขของข้อความลับ และ P เป็นตัวเลขของข้อความปกติ
การเข้ารหัสคือการเปลี่ยนข้อความปกติให้เป็นข้อความลับจะได้ว่า
อินพุต : ค่าตัวเลขประจำตัวอักษรของข้อความปกติ (P) และ และกุญแจ (k)
เอาท์พุต : ค่าตัวเลขประจำตัวอักษรข้อความลับ (C)
ฟังก์ชันเข้ารหัส: C = (P+k) mod 26
ตัวอย่างเช่นหากเราต้องการส่งข้อความ HELP
อินพุต : H = 8, E = 6, L = 12, P = 16, k = 20
เมื่อทำการเข้ารหัสจะได้
H = 8 => (8+20) mod 26 = 2 => B
E = 6 => (6+20) mod 26 = 0 หรือ 26 => Z
L = 12 => (12+20) mod 26 = 6 => F
P = 16 => (16+20) mod 26 = 10 => J
เอาท์พุต : BZFJ
การถอดรหัสคือการเปลี่ยนข้อความปกติให้เป็นข้อความลับจะได้ว่า
อินพุต : ค่าตัวเลขประจำตัวอักษรของข้อความลับ (Q) และ และกุญแจ (k)
เอาท์พุต : ค่าตัวเลขประจำตัวอักษรข้อปกติ (P)
ฟังก์ชันเข้ารหัส: P = (C-k) mod 26
ตัวอย่างเช่นหากเราต้องการถอดข้อความ BZFJ
อินพุต : B = 2, Z = 26, F = 6 , J = 10, k = 20
เมื่อทำการเข้ารหัสจะได้
B = 2 => (2-20) mod 26 = -18+26 = 8 => H
Z = 26 => (26-20) mod 26 = 6 => E
F = 6 => (6-20) mod 26 = -14+26 = 12 => L
J = 10 => (10-20) mod 26 = -10+26 =16 => P
เอาท์พุต : HELP
การเข้ารหัสถอดรหัสข้างต้นนั้นเป็นการเข้ารหัสถอด รหัสอย่างง่ายเรียกว่า อักษรซีซาร์ไซเฟอร์ นอกจากนี้ยังมีระบบการเข้ารหัสและถอดรหัสอีกหลายรูปแบบและมีความซับซ้อนมากขึ้นเพื่อความปลอดภัยหนึ่งในระบบการเข้ารหัสถอดรหัสที่นิยมเป็นการเข้ารหัสและถอดรหัสบนพื้นฐานทฤษฎีจำนวนถูกพัฒนาขึ้นในปี ค.ศ. 1976–1977 โดย 1) Ronald Rivest 2) Adi Shamir และ 3) Leonard Adleman นักคณิตศาสตร์และนักคอมพิวเตอร์ที่ทำงานใน M.I.T เป็นที่มาของการเข้ารหัสและถอดรหัส RSA
แหล่งที่มา
http://marcuscode.com/lang/python/functions สืบค้นเมื่อ 20 มีนาคม 2562.
Skvarcius R., Robinson W.B. (1986). Discrete mathematics with computer science applications. The Benjamin/Cummings Publishing Company.
Epp S.S. (2011). Discrete mathematics with applications, 4th edition. Brooks/Cole Cengage Learning.
กลับไปที่เนื้อหา



