ดาวเคราะห์ (The Planets)
ดาวเคราะห์ (The Planets)
ในภาษาอังกฤษคำว่า ดาวฤกษ์ (Star) และดาวเคราะห์ (Planet) เขียนแตกต่างกันชัดเจน แต่ภาษาไทยเราเรียกวัตถุที่เป็นจุดแสงทุกอย่างบนฟ้า ว่า 'ดาว' ก็เลยเกิดความสับสน ตำราเก่าๆ มักบอกว่า ดาวฤกษ์เป็นดาวที่มีแสงในตัวเองจึงมีแสงไม่คงที่ ส่วนดาวเคราะห์ไม่มีแสงในตัวเองต้องสะท้อนแสงจากดวงอาทิตย์ ทำให้เรามองเห็นเป็นแสงนวลมีความสว่างคงที่ ในความเป็นจริงสิ่งที่กล่าวมานี้ยอมรับไม่ได้ เนื่องจากมีดาวฤกษ์เพียงบางดวงที่มีความสว่างไม่คงที่ เช่น ดาวแปรแสง แต่ก็ไม่สามารถตรวจวัดได้ด้วยตาเปล่า ต้องใช้อุปกรณ์ทางวิทยาศาสตร์ตรวจวัดอย่างละเอียด การที่เรามองเห็นดาวกระพริบระยิบระยับนั้นเป็นเพราะบรรยากาศของโลกแปรปรวน ในวันที่อากาศไม่ดี ไม่ว่าจะเป็นดาวฤกษ์หรือดาวเคราะห์ย่อมมีแสงกระพริบด้วยกันทั้งนั้น เฉกเช่นเดียวกับการมองดูปลาในกระแสน้ำ หากเราขึ้นไปดูดาวบนยอดดอยสูงซึ่งมีบรรยากาศบางจะพบว่า ไม่ว่าจะเป็นดาวฤกษ์หรือดาวเคราะห์ต่างก็ส่องแสงนวลไม่กระพริบ เราไม่สามารถจำแนกดาวฤกษ์และดาวเคราะห์ได้ด้วยวิธีนี้
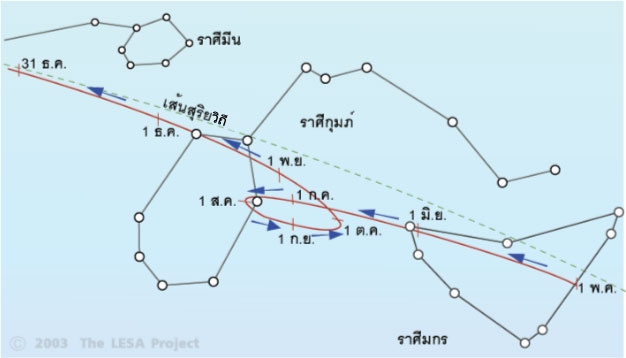
นิยามที่แท้จริงของดาวเคราะห์ คือ การเคลื่อนที่ คำว่า 'ดาวเคราะห์' หรือ 'Planet' มีรากศัพท์มาจากภาษาคำว่า 'Wander' ในภาษาละตินซึ่งแปลว่า ผู้สัญจร หรือ นักเดินทาง ดาวฤกษ์เป็นดาวประจำที่ เมื่อมองจากโลกของเราจะเห็นเป็นกลุ่มดาวซึ่งมีรูปร่างคงที่ไม่เปลี่ยนแปลง (ความเป็นจริงดาวฤกษ์ทั้งหลายเคลื่อนที่ไปตามการหมุนของกาแล็กซี ถ้าหากมองดูในช่วงเวลาพันปี ก็จะเห็นว่ากลุ่มดาวมีรูปร่างเปลี่ยนไปเล็กน้อย) ส่วนดาวเคราะห์จะเคลื่อนที่เปลี่ยนตำแหน่งไปในแต่ละวัน ภาพที่ 2 แสดงให้เห็นตำแหน่งของดาวอังคารบนท้องฟ้าซึ่งเปลี่ยนที่ไปในวันเมื่อเทียบกับกลุ่มดาวจักราศีที่อยู่ด้านหลัง
ภาพที่ 1 การเคลื่อนที่ของดาวอังคารผ่านหน้ากลุ่มดาวจักราศี
ในยุคโบราณเชื่อว่า โลกคือศูนย์กลางจักรวาล มีดาวทั้งหลายโคจรล้อมรอบจากทิศตะวันออกไปยังทิศตะวันตก ดาวทั้งหลายมีตำแหน่งคงที่เป็นรูปกลุ่มดาว ขึ้นตกตามเวลาที่แน่นอนของแต่ละฤดูกาล และเรียกดาวประเภทนี้ว่า 'ดาวฤกษ์' ส่วนดาวที่เคลื่อนที่เปลี่ยนตำแหน่งไปบนท้องฟ้าตามแนวสุริยวิถีเรียกว่า 'ดาวเคราะห์' ดังนั้นดาวเคราะห์ในยุคโบราณจึงมี 7 ดวงได้แก่ ดวงอาทิตย์ ดวงจันทร์ ดาวอังคาร ดาวพุธ ดาวพฤหัสบดี ดาวศุกร์ และดาวเสาร์ ซึ่งเป็นชื่อของวันในสัปดาห์ และเรียกกลุ่มดาวฤกษ์12 กลุ่มที่ดาวเคราะห์เคลื่อนที่ผ่านว่า “จักราศี” (Zodiac) ซึ่งเป็นชื่อเดือน
จนกระทั่งคริสต์ศตวรรษที่ 16 (พุทธศตวรรษที่ 21) เมื่อโคเปอร์นิคัสและกาลิเลโอค้นพบ หลักฐานที่ยืนยันว่า ดวงอาทิตย์เป็นศูนย์กลางของระบบสุริยะ มีโลกและดาวเคราะห์บริวารโคจรล้อมรอบ ดาวเคราะห์ในยุคนั้นจึงเหลือเพียง 6 ดวง ได้แก่ ดาวพุธ ดาวศุกร์ โลก ดาวอังคาร ดาวพฤหัสบดี และดาวเสาร์ เนื่องจากดวงอาทิตย์ถูกยกฐานะเป็นดาวฤกษ์ และดวงจันทร์ถูกลดสถานะเป็นบริวารของโลก
ต่อมาในปี ค.ศ.1781 (พ.ศ.2324) วิลเลียม เฮอร์สเชล นักดาราศาสตร์ชาวอังกฤษได้ส่องกล้องโทรทรรศน์ค้นพบดาวเคราะห์ดวงที่ 7 คือ ดาวยูเรนัส และในปี ค.ศ. 1801 (พ.ศ. 2344) ได้มีการค้นพบดาวเคราะห์น้อยดวงแรกชื่อ ซีรีส (Ceres) ซึ่งนักดาราศาสตร์ก็จัดให้เป็นดาวเคราะห์ดวงที่ 8 ตามมาด้วยการค้นพบ พาลาส (Pallas) จูโน (Juno) และ เวสตา (Vesta) ทำให้ภายในเวลาไม่ถึง 10 ปี สมาชิกดาวเคราะห์ในระบบสุริยะขยายตัวจาก 7 ดวงเป็น 11 ดวง ซึ่งก็อยู่ในวิสัยที่วงการยัง "รับได้" แต่นั่นคือหากเราเป็นนักเรียนที่เกิดในยุคนั้น ก็คงจะต้องท่องชื่อสมาชิกในระบบสุริยะว่า "ดาวพุธ ศุกร์ โลก อังคาร ซีรีส พาลาส จูโน เวสตา พฤหัสบดี เสาร์ และ ยูเรนัส" (ดาวเนปจูนยังไม่พบจนกระทั่งปี พ.ศ.2389)
ปัญหาสมาชิกระบบสุริยะในยุคนั้นลุกลามใหญ่โต 50 ปีภายหลังจากการค้นพบซีรีสได้มีการค้นพบวัตถุเหล่านี้เพิ่มขึ้นรวมเป็น 15 ดวง นักเรียนยุคนั้นก็คงต้องท่องชื่อดาวเคราะห์ทั้งหมด 23 ดวง เมื่อถึงจุดนี้นักดาราศาสตร์ต่างมีความเห็นตรงกันว่าดาวเคราะห์ขนาดเล็กมีมากเกินไป ดังนั้นในปี พ.ศ.1852 (พ.ศ. 2395) จึงมีการตั้งนิยามเพื่อแบ่งดาวเคราะห์ในยุคนั้นออกเป็น "ดาวเคราะห์หลัก" (Major Planet หรือเรียกอย่างสั้นว่า Planet) และ "ดาวเคราะห์น้อย" (Minor Planet) ต่อมาได้มีการค้นพบแถบดาวเคราะห์น้อย (Asteroid Belt) ระหว่างวงโคจรของดาวอังคารและดาวพฤหัสบดี นักดาราศาสตร์จึงนิยมเรียกดาวเคราะห์น้อยขนาดเล็กว่า "Asteroids"
ภาพที่ 2 เปรียบเทียบขนาดดาวเคราะห์น้อยกับดาวอังคาร (ที่มา: University of Hawaii)
เนื่องจากในปัจจุบันเทคโนโลยีด้านดาราศาสตร์ก้าวหน้าไปมาก มีทั้งการสร้างกล้องโทรทรรศน์ขนาดใหญ่ และกล้องโทรทรรศน์อวกาศซึ่งสามารถมองเห็นวัตถุในช่วงคลื่นต่างๆ โดยเฉพาะกล้องโทรทรรศน์อินฟราเรดซึ่งช่วยให้นักดาราศาสตร์ตรวจพบวัตถุที่มี อุณหภูมิต่ำและมีขนาดเล็กได้ ในทศวรรษที่ผ่านมาได้มีการค้นพบดาวเคราะห์ที่มีขนาดใกล้เคียงกับดาวพลูโตอีก หลายดวง เช่น เซดนา ออร์คัส ดังที่แสดงในภาพที่ 3 นอกจากนั้นยังมีการค้นพบดาวเอริสซึ่งมีขนาดใหญ่กว่าดาวพลูโต
ภาพที่ 3 ขนาดของดาวเคราะห์แคระเปรียบเทียบกับโลก (ที่มา: NASA, JPL)
ในวันที่ 24 สิงหาคม 2549 สมาพันธ์ดาราศาสตร์สากล (IAU) ได้ประกาศลดสถานะดาวพลูโต ให้เป็นดาวเคราะห์แคระทั้งนี้เนื่องจาก ดาวพลูโตก็เป็นเพียงวัตถุวัตถุหนึ่งในระบบสุริยะ ไม่ต่างจากดาวเคราะห์น้อยที่โคจรรอบดวงอาทิตย์ ซึ่งค้นพบแล้วกว่า 338,100 ดวง (ข้อมูล ณ วันที่ 9 สิงหาคม 2549) และยังมีการค้นพบเพิ่มขึ้นอย่างต่อเนื่องกว่า 4,000 ดวงต่อเดือน สมาพันธ์ดาราศาสตร์สากลได้ปรับนิยามใหม่ของดาวเคราะห์ ดังนี้
1. ดาวเคราะห์ (Planet) หมายถึง เทห์วัตถุที่มีสมบัติดังต่อไปนี้ครบถ้วน
(ก) โคจรรอบดวงอาทิตย์
(ข) มีมวลมากพอที่จะแรงโน้มถ่วงของดาวสามารถเอาชนะความแข็งของเนื้อดาว ส่งผลให้ดาวอยู่ในสภาวะสมดุลไฮโดรสแตติก (hydrostatic equilibrium; เช่น ทรงเกือบกลม)
(ค) สามารถกวาดเทห์วัตถุในบริเวณข้างเคียงไปได้
2. ดาวเคราะห์แคระ (Dwarf Planet) หมายถึง เทห์วัตถุที่มีสมบัติดังต่อไปนี้ครบถ้วน
(ก) โคจรรอบดวงอาทิตย์
(ข) มีมวลมากพอที่จะแรงโน้มถ่วงของดาวสามารถเอาชนะความแข็งของเนื้อดาว ส่งผลให้ดาวอยู่ในสภาวะไฮโดรสแตติก (hydrostatic equilibrium; เช่น ทรงเกือบกลม)
(ค) ไม่สามารถกวาดเทห์วัตถุในบริเวณข้างเคียงไปได้
(ง) ไม่ใช่ดวงจันทร์บริวารของดาวเคราะห์อื่นๆ
3. เทห์วัตถุขนาดเล็กในระบบสุริยะ (Small Solar-System Bodies) หมายถึง วัตถุอื่นๆ นอกเหนือจากที่กล่าวไปแล้ว
จึงสรุปได้ว่า ในปัจจุบันระบบสุริยะมีดาวเคราะห์ 8 ดวง คือ ดาวพุธ ดาวศุกร์ โลก ดาวอังคาร ดาวพฤหัสบดี ดาวเสาร์ ดาวยูเรนัส ดาวเนปจูน และมีดาวเคราะห์แคระอีกหลายดวงที่รู้จักกันดี เช่น ดาวพลูโตเคยถูกจัดเป็นดาวเคราะห์ดวงที่ 9 ดาวซีรีสเคยถูกจัดว่าเป็นดาวเคราะห์น้อยที่ใหญ่ที่สุด ดาวเอริสซึ่งมีขนาดใหญ่กว่าดาวพลูโต
ที่มา
http://www.lesa.biz/astronomy/cosmos/planet-definition
กลับไปที่เนื้อหา
การเคลื่อนที่ของดาวเคราะห์ ระบบดวงอาทิตย์เป็นศูนย์กลาง
มนุษย์ พยายามจะทำความเข้าใจเรื่องจักรวาล โดยทำการศึกษาการเคลื่อนที่ของวัตถุท้องฟ้ามาแต่โบราณ ประมาณ 800 ปีก่อนคริสตกาล ชาวบาบีโลนได้สร้างปฏิทินโดยการศึกษาการเคลื่อนที่ของดาวเคราะห์ผ่านหน้า กลุ่มดาวจักราศี 12 กลุ่ม พวกเขาได้ตั้งชื่อ ดวงอาทิตย์ ดวงจันทร์ และดาวเคราะห์ที่มองเห็นด้วยตาเปล่าทั้งห้าดวง ขึ้นเป็นชื่อวันในสัปดาห์ วันอาทิตย์, วันจันทร์, วันอังคาร, ... ถึง วันเสาร์ ตามที่เราได้ใช้กันอยู่ตราบจนทุกวันนี้
600 ปีก่อนคริสตกาล พีธากอรัส (Pythagoras) นักปราชญ์ชาวกรีกได้สร้างแบบจำลองของจักรวาล แสดงตำแหน่งของโลก ตั้งอยู่ ณ ศูนย์กลางซึ่งล้อมรอบด้วยทรงกลมฟ้า (Celestial sphere) อันเป็นที่ตีั้งของดวงดาวทั้งหลาย ทรงกลมฟ้าซึ่งเคลื่อนที่ในทิศตรงกันข้ามกับดวงอาทิตย์และดวงจันทร์ ดังภาพที่ 1
ภาพที่ 1 แบบจำลองระบบจักรวาลของพีธากอรัส
สองร้อยห้าสิบปีต่อมา (250 ปีก่อนคริสตกาล) อริสโตเติล (Aristotle) นักปราชญ์ชาวกรีกผู้มีชื่อเสียง ได้ปรับปรุงแบบจำลองระบบสุริยะของพิธากอรัส โดยเพิ่มทรงกลมใสข้าง ในอีก 7 ชั้น เพื่อเป็นที่ตั้งของ ดวงอาทิตย์ ดวงจันทร์ และดาวเคราะห์ที่มองเห็นด้วยตาเปล่าอีก 5 ดวง ได้แก่ ดาวพุธ ดาวศุกร์ ดาวอังคาร ดาวพฤหัสบดี และดาวเสาร์ ทรงกลมทั้งเจ็ดเคลื่อนที่สวนทางกับทรงกลมท้องฟ้า และเคลื่อนที่จากทางทิศตะวันตกไปยังทิศตะวันออกด้วยความเร็วที่แตกต่างกันไป อริสโตเติลให้ความเห็นว่า ดวงอาทิตย์และดวงจันทร์เป็นทรงกลมที่สมบูรณ์ (มีผิวเรียบ) ทั้งดาวฤกษ์ ดวงอาทิตย์ ดวงจันทร์ และดาวเคราะห์ต่างเคลื่อนที่รอบโลกซึ่งเป็นศูนย์กลางของจักรวาล การเคลื่อนที่ของวัตถุบนโลกมีสองชนิด คือ การเคลื่อนที่ในแนวราบเรียกว่า 'แรง' (Force) ส่วนการเคลื่อนที่ในแนวดิ่งเป็น 'การเคลื่อนที่ตามธรรมชาติ' (Natural motion) มิได้มีแรงอะไรมากระทำ ทุกสรรพสิ่งต้องเคลื่อนที่เข้าหาศูนย์กลางของโลกเนื่องจาก 'โลกเป็นศูนย์กลางของจักรวาล' (Geocentric)
ภาพที่ 2 ระบบโลกเป็นศูนย์กลางของอริสโตเติล
ปี ค.ศ. 125 (พ.ศ. 668) คลอเดียส ทอเลมี (Claudius Ptolemy) นักดาราศาสตร์ชาวกรีก ได้ปรับปรุงแบบจำลองของอริสโตรเติลให้สอดคล้องกับผลที่ได้จากการสังเกตการณ์ เขาสังเกตว่าในบางครั้งดาวเคราะห์เคลื่อนที่ถอยหลัง (Retrograde motion) เมื่อเทียบกับกลุ่มดาวจักราศีที่อยู่ด้านหลัง ดังภาพที่ 3
ภาพที่ 3 การเคลื่อนที่ย้อนทาง (Retrograde motion)
ทอเลมี เขียนตำราดาราศาสตร์ฉบับแรกของโลกชื่อ 'อัลมาเจสท์' (Almagest) โดยใช้หลักการเรขาคณิตอธิบายว่า โลกเป็นทรงกลมหยุดนิ่งอยู่กับที่ตรงศูนย์กลางของจักรวาล มีดาวเคราะห์ทั้งเจ็ด ได้แก่ ดวงอาทิตย์ ดวงจันทร์ และดาวเคราะห์ห้าดวงที่มองเห็นด้วยตาเปล่า เป็นบริวารโคจรล้อมรอบ ปรากฏการณ์ดาวเคราะห์เคลื่อนที่สวนทางกับกลุ่มดาวจักราศี (Retrograde motion) เกิดขึ้นเนื่องจาก ดาวเคราะห์ทั้งเจ็ดเคลื่อนที่อยู่บนวงกลมขนาดเล็กเรียกว่า 'เอปิไซเคิล' (Epicycle) ซึ่งวางอยู่ บนวงโคจรรอบโลกอีกทีหนึ่ง ดังที่แสดงในภาพที่ 4 ทอเลมีไม่ได้อธิบายถึงมูลเหตุของวงกลมเล็ก เขาเพียงสร้างวงกลมเล็กขึ้นเพื่อเป็นทางออกสำหรับคำตอบในสิ่งที่เขาเห็น อย่างไรก็ตามแบบจำลองนี้เป็นที่ยอมรับกันเป็นเวลาหนึ่งพันปีกว่าต่อมา ก่อนที่จะถูกค้านโดย นิโคลัส โคเปอร์นิคัส
ภาพที่ 4 ระบบโลกเป็นศูนย์กลางของทอเลมี
ในปี ค.ศ. 1576 (พ.ศ. 2119) ไทโค บราฮ์ (Tycho Brahe) นักดาราศาสตร์ชาวเดนมาร์กได้สร้างหอดูดาว Uraniborg เพื่อ ติดตั้ง ควอดแดรนท์ (Quadrant) ซึ่งเป็นอุปกรณ์วัดมุมดาวขนาดรัศมี 1.96 เมตร ดังแสดงในภาพที่ 5 เพื่อทำการวัดตำแหน่งการเคลื่อนที่ของดาวเคราะห์อย่างละเอียด โดยมี โจฮานเนส เคปเลอร์ (Johannes Kepler) นักคณิตศาสตร์ชาวเยอรมันเป็นผู้ช่วยวิเคราะห์ข้อมูล
ภาพที่ 5 ควอดแดรนท์ของไทโค
แม้ว่าจะทำการตรวจวัดตำแหน่งของดาวเคราะห์อย่างละเอียด ไทโคก็ยังเชื่อในแบบจำลองระบบสุริยะของเขาว่า ดวงอาทิตย์และดวงจันทร์โคจรรอบโลก โดยที่ดาวเคราะห์ทั้งห้า ซึ่งได้แก่ ดาวพุธ ดาวศุกร์ ดาวอังคาร ดาวพฤหัสบดี และดาวเสาร์โคจรล้อมรอบดวงอาทิตย์ ดังที่แสดงในภาพที่ 6 อย่างไรก็ตามในเวลาต่อมาไม่นาน โจฮานเนส เคปเลอร์ ได้ประกาศ กฎการเคลื่อนที่ของดาวเคราะห์รอบดวงอาทิตย์
ภาพที่ 6 ระบบโลกเป็นศูนย์กลางของไทโค
ที่มา
http://www.lesa.biz/astronomy/cosmos/geocentric
กลับไปที่เนื้อหา
การเคลื่อนที่ของดาวเคราะห์ ระบบโลกเป็นศูนย์กลาง
ในยุคกรีกโบราณ คนส่วนใหญ่เชื่อในระบบโลกเป็นศูนย์กลางของจักรวาล (Geocentric) ของอริสโตเติล อย่างไรก็ตามนักปราชญ์บางคนมีความคิดเห็นตรงกันข้าม อริสตาร์คัส (Aristarchus) นักเรขาคณิตชาวกรีกแห่งเมืองอเล็กซานเดรีย (อยู่ในประเทศอียิปต์ในปัจจุบัน) ได้เสนอแบบจำลองของจักรวาลซึ่งมี 'ดวงอาทิตย์เป็นศูนย์กลาง' (Heliocentric) โดยอธิบายว่า โลกหมุนรอบตัวเองวันละ 1 รอบ จากทิศตะวันตกไปยังทิศตะวันออก ทำให้เรามองเห็นท้องฟ้าเคลื่อนที่จากทิศตะวันออกไปยังทิศตะวันตก ขณะเดียวกันโลกก็โคจรไปรอบดวงอาทิตย์ ทำให้เรามองเห็นดวงอาทิตย์เคลื่อนที่ผ่านหน้ากลุ่มดาวจักราศีทั้งสิบสอง อริสตาร์คัสคำนวณเปรียบเทียบได้ว่า ดวงอาทิตย์มีขนาดใหญ่กว่าโลก โลกอยู่ใกล้ดวงจันทร์แต่อยู่ไกลจากดวงอาทิตย์ ถึงกระนั้นก็ตามแนวความคิดนี้ยังไม่เป็นที่ยอมรับของคนในยุคนั้น เพราะเป็นสิ่งที่ขัดแย้งกับการมองเห็น ยากต่อจินตนาการ และยังไม่มีใครพิสูจน์ได้ ประกอบกับโชคไม่ดีที่ห้องสมุดอเล็กซานเดรียถูกไฟใหม้ ตำราที่อริสตาร์คัสเขียนขึ้น ถูกทำลายจนหมดสิ้น มีแต่หลักฐานที่เกี่ยวข้องจากผู้ที่อยู่ร่วมยุคสมัยเท่านั้นที่เหลืออยู่
ภาพที่ 1 นิโคลาส โคเปอร์นิคัส
ปี ค.ศ. 1514 (พ.ศ. 2057) นิโคลาส โคเปอร์นิคัส (Nicolaus Copernicus) บาทหลวงชาวโปแลนด์ เป็นผู้มีประสบการณ์ในการติดตามการเคลื่อนที่ของดาวเคราะห์เป็นเวลา 20 ปี มีความคิดขัดแย้งกับระบบโลกเป็นศูนย์กลาง เขาให้ความเห็นว่า การอธิบายการเคลื่อนที่ถอยหลังของดาวเคราะห์ โดยใช้วงกลมเล็กในแบบจำลองของทอเลนั้น เลื่อนลอยไร้เหตุผล เขาได้เขียนหนังสือชื่อ De revolutionibus orbium coelestium (ปฏิวัติความเชื่อเรื่องท้องฟ้า) นำเสนอแนวความคิดที่มีระบบดวงอาทิตย์เป็นศูนย์กลาง (Heliocentric) ดังภาพที่ 2 อธิบายดังนี้
I. วงโคจรของดาวฤกษ์
II. วงโคจรของดาวเสาร์
III. วงโคจรของดาวพฤหัสบดี
IIII. วงโคจรของดาวอังคาร
V. วงโคจรของโลกและดวงจันทร์
VI. วงโคจรของดาวศุกร์
VII. วงโคจรของดาวพุธ
จุดศูนย์กลางคือดวงอาทิตย์
ภาพที่ 2 แบบจำลองระบบสุริยะของโคเปอร์นิคัส
หนังสือเล่มนี้ซึ่งถือเป็นจุดเริ่มต้นของดาราศาสตร์ยุคใหม่ ดังนี้
- ทรงกลมฟ้า (ซึ่งเป็นที่ตั้งของดาวฤกษ์ และดาวเคราะห์) เคลื่อนที่รอบดวงอาทิตย์ โดยมีดวงอาทิตย์อยู่ที่ศูนย์กลางของจักรวาล
- ระยะทางจากโลกไปยังทรงกลมฟ้าอยู่ไกลกว่าระยะทางจากโลกไปยังดวงอาทิตย์
- การเคลื่อนที่ปรากฏของทรงกลมฟ้าสัมพัทธ์กับเส้นขอบฟ้าในแต่ละวัน เป็นผลจากการที่โลกหมุนรอบตัวเอง
- การเคลื่อนที่ย้อนกลับของดาวเคราะห์ (Retrograde motion) เกิดขึ้นเนื่องจากการเคลื่อนที่ไปตามวงโคจรของโลกสัมพัทธ์กับการเคลื่อนที่ไปตามวงโคจรของดาวเคราะห์ วงกลมเล็ก (Epicycle) ของทอเลมีมิได้มีอยู่จริง
ภาพที่ 3 การเคลื่อนที่ย้อนกลับของดาวเคราะห์เป็นเพียงภาพสัมพัทธ์
โคเปอร์นิคัสอธิบายการมองเห็นการเคลื่อนที่ย้อนกลับของดาวอังคารในภาพที่ 3 ว่า วงโคจรรอบดวงอาทิตย์ของโลกมีขนาดเล็กกว่าวงโคจรของดาวอังคาร ดาวอังคารจึงต้องใช้คาบเวลาในการโคจรรอบดวงอาทิตย์นานกว่าโลก เมื่อโลกเคลื่อนที่แซงดาวอังคาร เราจะมองเห็นดาวอังคารเคลื่อนที่ย้อนกลับ เมื่อเปรียบเทียบกับทิศทางการเคลื่อนที่ของกลุ่มดาวทั้งหลายที่อยู่บนทรงกลมฟ้า
ที่มา
http://www.lesa.biz/astronomy/cosmos/heliocentric
กลับไปที่เนื้อหา
กาลอวกาศโค้ง
ดาฟิด ฮิลแบร์ท
https://th.wikipedia.org/wiki/
ภาพถ่ายของอัลเบิร์ต ไอน์สไตน์ ขณะมีอายุ 42 ปี
https://th.wikipedia.org/wiki/
อัลเบิร์ต ไอน์สไตน์ ตีพิมพ์ทฤษฎีสัมพัทธภาพทั่วไป ในปี พ.ศ. 2459 (ค.ศ. 1916) (นำเสนอเป็นปาฐกถาในสถาบันวิทยาศาสตร์รัสเซียเมื่อวันที่ 15 พฤศจิกายน พ.ศ. 2458) อย่างไรก็ตาม เดวิด ฮิลเบิร์ต นักคณิตศาสตร์ชาวเยอรมัน เคยเขียนและนำเสนอสมการคล้ายคลึงกันก่อนหน้าไอน์สไตน์ แต่ไม่ได้หมายความว่าเป็นการคัดลอกกันแต่อย่างใด กล่าวได้ว่าทั้งสองต่างเป็นผู้ให้กำเนิดทฤษฎีสัมพัทธภาพทั่วไปร่วมกัน
ทฤษฎีนี้กล่าวถึงสมการหนึ่งที่มาแทนที่กฎแรงโน้มถ่วงของนิวตัน ใช้เรขาคณิตเชิงอนุพันธ์และเทนเซอร์ในการอธิบายความโน้มถ่วง แสดงให้เห็นว่าผู้สังเกตทุกคนเหมือนกันไม่ว่าจะเคลื่อนที่ด้วยอัตราเร็วคงที่หรือไม่ กฎของทฤษฎีสัมพัทธภาพทั่วไปเหมือนกันสำหรับผู้สังเกตทุกคน แม้ว่าผู้สังเกตแต่ละคนเคลื่อนที่ด้วยความเร่งเมื่อเทียบกับผู้สังเกตคนอื่น ในทฤษฎีสัมพัทธภาพทั่วไป ความโน้มถ่วงไม่ได้เป็นแรง (อย่างในกฎความโน้มถ่วงของนิวตัน) อีกต่อไป แต่เป็นผลจากการโค้งของกาล-อวกาศ (spacetime หรืออาจแปลว่าปริภูมิก็ได้) ทฤษฎีสัมพัทธภาพทั่วไปเป็นทฤษฎีเชิงเรขาคณิตที่ถือหลักว่ามวลและพลังงานทำให้เกิดการโค้งงอของกาล-อวกาศ และการโค้งนี้ส่งผลต่อเส้นทางการเคลื่อนที่ของอนุภาคอิสระรวมทั้งแสง
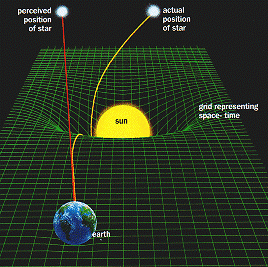
ภาพลำแสงโค้งเมื่อผ่านวัตถุขนาดใหญ่ เช่น ดวงอาทิตย์ เป็นต้น
https://www.gotoknow.org/posts/440419
การพิสูจน์กาลอวกาศโค้ง
แม้จะผ่านมาเป็น 100 ปีแต่ทฤษฎีของไอน์สไตน์ก็ยังต้องได้รับพิสูจน์กันต่อไป ล่าสุดการทดลองอันยาวนานของนาซาได้ยืนยัน 2 คำทำนายสำคัญตามทฤษฎีสัมพัทธภาพทั่วไป และเป็นครั้งแรกที่ยืนยันได้ว่ากาล-อวกาศบิดเบี้ยวไปตามการหมุนของวัตถุ ซึ่งเป็นการย้ำอย่างชัดเจนว่านักฟิสิกส์ชาวยิวผู้นี้ยังคงถูกต้อง
การยืนยันล่าสุดในทฤษฎีสัมพัทธภาพทั่วไป (General Relativity หรือ GR) ซึ่งเป็นทฤษฎีของความโน้มถ่วง (Gravity) ของ อัลเบิร์ต ไอน์สไตน์ (Albert Einstein) ว่ายังคงถูกต้องนั้น เป็นผลการสังเกตการณ์ของยานอวกาศกราวิตี โพรบ บี (Gravity Probe B) ขององค์การบริหารการบินอวกาศสหรัฐฯ (นาซา) ซึ่งถูกส่งขึ้นไปตั้งแต่ 20 เม.ย.2004 เพื่อสังเกตปรากฏการณ์ตามคำทำนายจากทฤษฎีที่เขาเสนอมาตั้งแต่ปี 1916
ตรวจหาอวกาศโค้งงอและบิดเบี้ยว
ตามคำทำนายของทฤษฎีสัมพัทธภาพทั่วไป กาลเวลา (time) และอวกาศ (space) จะบิดเบี้ยวไป เนื่องจากการมีอยู่ของวัตถุขนาดใหญ่อย่างดาวเคราะห์และดวงดาวต่างๆ และเพื่อพิสูจน์ความถูกต้องของทฤษฎี ยานกราวิตีโพรบบี หรือ จีพี-บี (GP-B) จึงถูกส่งขึ้นไปตรวจวัดปรากฏการณ์ที่เป็นผลจากวัตถุขนาดใหญ่อย่างเช่นโลกได้ 2 ปรากฏการณ์ด้วยกัน
นั่นคือ ปรากฏการณ์จีโอเดติก (geodetic effect) ที่กาลอวกาศโค้งงออันเนื่องจากการมีอยู่ของวัตถุขนาดใหญ่ และเมื่อโลกหรือวัตถุขนาดใหญ่อื่นๆ หมุนจะทำให้กาลอวกาศบิดเบี้ยวในลักษณะของการ 'ลาก' (dragging) กาลอวกาศไป ซึ่งเรียกปรากฏการณ์ดังกล่าวว่า ปรากฏการณ์เฟรมแดรกกิง (frame-dragging effect) หรือปรากฎการณ์การลากกรอบอ้างอิง ซึ่งไม่มีปรากฏการณ์เหล่านี้ในแนวคิดของ เซอร์ไอแซค นิวตัน (Sir Isaac Newton) เพราะอวกาศในแนวคิดของนิวตันนั้นสมบูรณ์และไม่โค้งงอ
"ในเอกภพของไอน์สไตน์ 'กาล' (time) และ 'อวกาศ' (space) โค้งงอด้วยแรงโน้มถ่วง โลกของเราได้ทำให้อวกาศที่อยู่โดยรอบโค้งงอเล็กน้อยๆ ด้วยแรงโน้มถ่วงของโลกเราเอง ลองจินตนาการว่าโลกแช่อยู่ในน้ำผึ้ง เมื่อโลกหมุน น้ำผึ้งที่อยู่รอบๆ ก็บิดตาม ซึ่งก็เป็นอย่างเดียวกับที่เกิดขึ้นกับกาลและอวกาศ" ศ.ฟรานซิส เอเวอริตต์ (Prof.Francis Everitt) นักฟิสิกส์จากมหาวิทยาลัยแสตนฟอร์ด (Stanford University) สหรัฐฯ และผู้ตรวจสอบหลักในโครงการยานกราวิตีโพรบบีอธิบาย
ยานกราวิตีโพรบบีถูกส่งขึ้นไปพร้อมกับไจโรสโคป (gyroscope) หรือลูกข่างวัดการหมุนที่มีความแม่นยำมากถึง 4 ตัว ซึ่งไจโรสโคปทั้งหมดจะหมุนโดยมีดาว ไอเอ็ม เปกาซี (IM Pegasi) หรือ เอชอาร์ 8703 (HR 8703) เป็นจุดอ้างอิงของแกนหมุน การเลื่อนของแกนหมุนเพียงเล็กน้อยเป็นสิ่งยืนยันว่าไอน์สไตน์ถูกต้อง แต่หากไอน์สไตน์ผิดไจโรสโคปจะหมุนอย่างมั่นคง
หัวใจการทดลองอยู่ที่ 'ไจโรสโคป'
ข้อมูลจากศูนย์การบินอวกาศมาร์แชลล์ (Marshall Space Flight Center) ของนาซาระบุว่า ไจโรสโคปแต่ละตัวประกอบด้วยลูกบอลขนาด 38 มิลลิเมตร ที่ทำจากแร่ควอตซ์เคลือบนิโอเบียม ควอตซ์เป็นธาตุที่มีความเสถียรในหลายช่วงอุณหภูมิ ยืดและหดตัวน้อย ไจโรสโคปทั้งหมดถูกจัดวางเรียงเป็นแถว มี 2 ตัวที่หมุนตามเข็มนาฬิกาและอีก 2 ตัวหมุนทวนเข็มนาฬิกา
เพื่อผลการทดลองที่แม่นยำลูกบอลทรงกลมจะถูกรักษาไว้ที่ความเย็นใกล้ 'ศูนย์องศาสัมบูรณ์' (absolute zero) หรือประมาณ -273 องศาเซลเซียส ภายในกระบอกสุญญากาศขนาดใหญ่ที่บรรจุฮีเลียมในสถานะของไหลยิ่งยวด (super-fluid) ซึ่งช่วยปกป้องกันสิ่งรบกวนจากภายนอก ทั้งความดัน ความร้อน สนามแม่เหล็ก แรงโน้มถ่วง และประจุไฟฟ้า
ไจโรสโคปและกล้องโทรทรรศน์ตามดาวถือเป็นหัวใจสำคัญของยานกราวิตีโพรบ บี ซึ่งโคจรรอบโลกในแนวขั้วโลกเหนือ-ขั้วโลกใต้อยู่ที่ระดับความสูง 642 กิโลเมตร โดยคาดว่าผลจากปรากฏการณ์เฟรมแดรกกิงจะทำให้แกนหมุนของไจโรสโคปในระนาบการหมุนของโลกเปลี่ยนไปปีละ 0.014 ฟิลิปดา หรือ 0.000011 องศา ซึ่งยังไม่มีเคยมีการวัดปรากฏการณ์นี้ได้มาก่อน
จากการวิเคราะห์ข้อมูลที่เก็บรวบรวมตั้งแต่ 28 ส.ค. 2004 ถึง 14 ส.ค. 2005 ทีมวิจัยของ ศ.เอเวอร์ริตต์ พบว่าแกนหมุนของไจโรสโคปเลื่อนไปด้วยอัตรา 6,601.818.3 มิลลิฟิลิปดาต่อปี (mas/yr) * จากปรากฏการณ์จิโอเดติก ส่วนการเลื่อนของแกนหมุนจากปรากฏการณ์เฟรมแดรกกิงอยู่ที่ 37.27.2 มิลลิฟิลิปดาต่อปี เปรียบเทียบกับคำทำนายตามทฤษฎีที่ว่าปรากฏการณ์จีโอเดติกจะทำให้แกนหมุน เลื่อนไป 6,606.1 มิลลิฟิลิปดาต่อปี ส่วนผลจากเฟรมแดรกกิงอยู่ที่ 39.2 มิลลิฟิลิปดาต่อปี
ผลการวิเคราะห์ของทีมวิจัย ศ.เอเวอร์ริตต์ ครั้งนี้ ตีพิมพ์ลงวารสารวิชาการฟิสิคัลรีวิวเลตเตอร์ส (Physical Review Letters) อันมีชื่อเสียงซึ่งบีบีซีนิวส์ระบุถึงความสำคัญของงานวิจัยนี้ว่า นอกจากย้ำถึงความอัจฉริยะของไอน์สไตน์แล้ว ยังให้เครื่องมือที่มีความละเอียดมากขึ้นเพื่อทำความเข้าใจฟิสิกส์ที่ขับเคลื่อนจักรวาลด้วย
เตรียมการทดลองยาวนาน 4 ทศวรรษ
กว่าจะได้ส่งยานกราวิตีโพรบบีขึ้นไปพิสูจน์ทฤษฎีไอน์สไตน์ต้องใช้ เวลากว่า 4 ทศวรรษ โดยแนวคิดในการส่งไจโนสโคปขึ้นไปโคจรรอบโลกเพื่อพิสูจน์ทฤษฎีสัมพัทธภาพนั้น ถูกเสนอขึ้นช่วงปี 1959-1960 โดยนักฟิสิกส์ 2 คนคือ จอร์จ พัฟ (George Pugh) เลโอนาร์ด สชิฟฟ์ (Leonard Schiff) ซึ่งต่อมาชิฟฟ์ได้กลายเป็นอธิการบดีของมหาวิทยาลัยสแตนฟอร์ด
ในช่วงแรกโครงการนี้เป็นความร่วมมือระหว่างภาควิชาฟิสิกส์และภาควิชา อื่นภายในสแตนฟอร์ด จนกระทั่งปี 1971 การบริหารจัดการโครงการถูกโอนย้ายไปยังศูนย์การบินอวกาศมาร์แชลของนาซา ส่วน ศ.เอเวอร์ริตต์ ผู้วิเคราะห์ผลล่าสุดในการทดลองพิสูจน์ทฤษฎีของไอน์สไตน์ก็มีส่วนร่วมใน โครงการนี้มาตั้งแต่ต้น โดยเขาได้รับเชิญให้ไปทำงานที่สแตนฟอร์ดตั้งแต่ปี 1962 เพื่อร่วมโครงการนี้โดยมีสชิฟฟ์เป็นที่ปรึกษาโครงการ
แม้ว่าแนวคิดของปฏิบัติการนี้จะค่อนข้างเรียบง่าย โดยการทดลองต้องการเพียงดาวอ้างอิงการหมุน กล้องโทรทัศน์และพื้นที่ของการหมุน แต่หน่วยงานที่เกี่ยวข้องกับการทดลองนี้ต้องใช้เวลาหลายสิบปีเพื่อพัฒนาไจโร สโคปที่มีความแม่นยำสูง โดยลูกบอลของไจโรสโคปนี้ได้รับการบันทึกว่าเป็นลูกบอลที่กลมที่สุดในโลกที่ มนุษย์เคยสร้างขึ้น และยังต้องเตรียมเทคโนโลยีที่มีความก้าวหน้าเพื่อตอบสนองการทดลองที่ “เรียบง่าย” นี้
นักฟิสิกส์ไทยชี้ผลทดลองเป็นไปตามคาด
ในมุมของนักฟิสิกส์ไทย ดร.บุรินทร์ กำจัดภัย จากสถาบันสำนักเรียนท่าโพธิ์ฯ วิทยาลัยเพื่อการค้นคว้าระดับรากฐานแห่งมหาวิทยาลัยนเรศวร เผยกับทีมข่าววิทยาศาสตร์ ASTV-ผู้จัดการออนไลน์ว่า เขาไม่แปลกใจกับการทดลองนี้เพราะเชื่อมั่นอยู่แล้วว่าทั้ง 2 ปรากฏการณ์ที่กราวิตีโพรบบีพิสูจน์ไปนั้นน่าจะเป็นจริง แต่ก็พลอยรู้สึกตื่นเต้นยินดีไปด้วยกับผลการทดลองเช่นเดียวกับนักฟิสิกส์ ความโน้มถ่วงคนอื่นๆ ซึ่งก็น่าจะตื่นเต้นกับข้อมูลที่ได้จากปฏิบัติการในครั้งนี้ เพราะ เป็นครั้งแรกที่สามารถตรวจวัดปรากฏการณ์เฟรมแดรกกิงได้ ส่วนการโค้งงอของอวกาศนั้นยานแคสสินี (Cassini) ขององค์การอวกาศยุโรปเคยตรวจวัดได้ก่อนหน้านี้แล้ว
“ผมได้ยินเรื่องกราวิตีโพรบบีครั้งแรกเมื่อราวๆ 10 ปีก่อนครับ ตั้งแต่ครั้งยังเรียนอยู่ที่ต่างประเทศ ได้ยินว่ามีโครงการนี้และกำลังจะเริ่มส่งยานขึ้นไป ตอนนี้เพื่อนๆ นักทดลองและนักสัมพัทธภาพคนอื่นๆ คงจะตื่นเต้นกับข้อมูลนี้เพราะแรงโน้มถ่วงเป็นแรงที่มีขนาดอ่อนมากวัดได้ยาก และการยืนยันทฤษฎีสัมพัทธภาพทั่วไปนั้นไม่ใช่เรื่องง่ายเลย ข่าวนี้เป็นข่าวใหม่มากครับเพราะรายงานชิ้นนี้เพิ่งตีพิมพ์ในวารสารเมื่อวัน ที่ 1 พ.ค. นี้เอง ส่วนบทความก็เพิ่งจะปรากฏบนฐานข้อมูล arXiv ** เมื่อวันที่ 18 พ.ค.นี้” ดร.บุรินทร์กล่าว
ดร.บุรินทร์คิดว่า โดยประโยชน์ทางอ้อมแล้วการทำการทดลองของกราวิตีโพรบบีนี้ได้สะท้อนให้เห็น อย่างชัดเจนว่าการทดลองทางฟิสิกส์บริสุทธิ์เพื่อพิสูจน์ทฤษฎีรากฐานนี้ได้ กระตุ้นและเหนี่ยวนำให้มีการพัฒนาเทคโนโลยีการวัด ประดิษฐกรรมและเทคโนโลยีขั้นสูงอื่นๆที่มีความแม่นยำและละเอียดสูง วิทยาศาสตร์ทำให้เกิดเทคโนโลยี และเทคโนโลยีก็ได้ย้อนมาเกื้อหนุนต่อการทดลองทางวิทยาศาสตร์
นักฟิสิกส์ไทยคนเดิมบอกด้วยว่า สิ่งที่ยืนยันความถูกต้องของทฤษฎีไอน์สไตน์ครั้งแรกคือปรากฏการณ์ที่ดาวเคราะห์ หรือดาวพุธเลื่อนตำแหน่งระหว่างเกิดปรากฏการณ์สุริยุปราคาเต็มดวง ที่ เซอร์ อาร์เธอร์ เอดดิงตัน (Sir Arthur Eddington) เป็นผู้สังเกตพบเมื่อปี 1919 ซึ่งเป็นการยืนยันว่าอวกาศโค้งงอเพราะการมีอยู่ของมวลขนาดใหญ่ทำให้แสงเดิน ทางโค้งงอและเห็นตำแน่งดาวพุธเลื่อนไป และการสังเกตการณ์ของเอดดิงตันได้ทำให้ไอน์สไตน์โด่งดังขึ้นอย่างมาก
ส่วนความท้าทายต่อไปของนักฟิสิกส์ทดลองขั้นต่อไปก็คือ การวัดคลื่นความโน้มถ่วง ซึ่งคลื่นดังกล่าวจะเกิดขึ้นเมื่อมีการขยับ หรือกระเพิ่มของมวลสารขนาดมากๆ ซึ่งจะทำให้เกิดการกระเพื่อมของกาลอวกาศรอบๆ โดยนาซาและองค์การอวกาศยุโรป (อีซา) มีความร่วมมือกันเพื่อส่งยานอวกาศ 3 ลำในปฏิบัติการลีซา (Laser Interferometer Space Antenna: LISA) ขึ้นไปตรวจวัดคลื่นความโน้มถ่วง
ข้อมูลจาก
http://www.manager.co.th/science/viewnews.aspx?NewsID=9540000062665
https://www.gotoknow.org/posts/440419
https://th.wikipedia.org/wiki/
กลับไปที่เนื้อหา
กาลิเลโอกับการศึกษาดาวเคราะห์
ในต้นคริสต์ศตวรรษที่ 17 (พุทธศตวรรษที่ 22) กาลิเลโอ กาลิเลอี (Galileo Galilei) นักวิทยาศาสตร์ชาวอิตาลี ซึ่งมีชีวิตอยู่ในช่วง ค.ศ. 1564 - 1642 (พ.ศ. 2107 - 2185) ได้นำกล้องส่องทางไกลซึ่งประดิษฐ์คิดค้นโดยชาวฮอลแลนด์ มาประยุกต์สร้างขึ้นเป็นกล้องโทรทรรศน์ชนิดหักเหแสงเพื่อใช้ส่องดูวัตถุท้องฟ้า กาลิเลโอพบว่าพื้นผิวของดวงจันทร์เต็มไปด้วยหลุมขรุขระ พื้นผิวของดวงอาทิตย์มีจุด (Sunspots) และมิได้เป็นทรงกลมที่สมบูรณ์ (มีผิวราบเรียบ) ดังคำสั่งสอนของอริสโตเติล
ภาพที่ 1 กาลิเลโอ กาลิเลอี
กาลิเลโอได้ศึกษาดาวเคราะห์ต่าง ๆ และพบว่า ดาวพฤหัสบดีมีดวงจันทร์บริวาร 4 ดวง เขาเฝ้าบันทึกการเคลื่อนที่ของดวงจันทร์ทั้งสี่ด้วยการสเก็ตรูป (ภาพที่ 2) และสรุปว่า ดวงจันทร์ทั้งสี่มิได้โคจรรอบโลกแต่โคจรรอบดาวพฤหัสบดี สิ่งที่กาลิเลโอค้นพบขัดแย้งกับคำสอนของอริสโตเติลที่ว่า “โลกคือศูนย์กลางของจักรวาล วัตถุท้องฟ้าทุกอย่างโคจรรอบโลก”
ภาพที่ 2 การบันทึกตำแหน่งดวงจันทร์ของดาวพฤหัสบดี ของกาลิเลโอ
เมื่อกาลิเลโอใช้กล้องโทรทรรศน์ส่องมองดาวศุกร์ เขาพบว่าขนาดปรากฏของดาวศุกร์เปลี่ยนแปลงไปในแต่ละวันคล้ายข้างขึ้นข้างแรม ขนาดของเสี้ยวดาวศุกร์เปลี่ยนแปลงไปตามตำแหน่งในวงโคจรรอบดวงอาทิตย์ เมื่อดาวศุกร์โคจรอยู่ด้านเดียวกับโลก ดาวศุกร์จะปรากฏเป็นเสี้ยวขนาดใหญ่ดวงจันทร์ข้ามแรม เนื่องจากเรามองเห็นแต่ทางด้านหลังดาวศุกร์ แต่เมื่อดาวศุกร์โคจรไปอยู่อีกด้านหนึ่งของดวงอาทิตย์ ดาวศุกร์จะมีขนาดเล็กลงแต่ทำมุมสะท้อนแสงอาทิตย์เกือบเป็นวงกลม ดังที่แสดงในภาพที่ 3 สิ่งนี้เองที่เป็นหลักฐานยืนยันว่าทั้งโลกและดาวศุกร์ต่างโคจรรอบดวงอาทิตย์
ภาพที่ 3 ภาพปรากฏของดาวศุกร์
การค้นพบของกาลิเลโอจะถูกต้องตรงความเป็นจริงแต่ขัดแย้งกับคำสั่งสอนของศาสนาใน ยุคนั้น ตำราที่เขาเขียนจึงถูกอายัดและตัวเขาเองก็ถูกจองจำอยู่กับบ้านจนวันตาย จนกระทั่งสามร้อยปีต่อมาในเดือนตุลาคม ค.ศ.1992 (พ.ศ.2535) โบสถ์แห่งสำนักวาติกันได้ออกมาแถลงการณ์ยอมรับข้อผิดพลาดที่ปฏิบัติต่อกาลิ เลโอ
กา ลิเลโอ มิได้เป็นเพียงนักดาราศาสตร์ผู้เฝ้าสังเกตการณ์แต่ยังเป็นนักฟิสิกส์ยุคใหม่ อีกด้วย อริสโตเติลเคยอธิบายว่า “การที่สิ่งของตกลงสู่พื้นดินนั้น เป็นเรื่องของการเคลื่อนที่ตามธรรมชาติ โดยไม่มีเรื่องของแรงมาเกี่ยวข้อง หากเป็นเพราะโลกเป็นศูนย์กลางของจักรวาล ทุกสิ่งจึงต้องเคลื่อนที่เข้าสู่ศูนย์กลางของโลก” กาลิเลโอคิดแตกต่างออกไป เขาเชื่อว่าการที่วัตถุตกลงสู่พื้นนั้นเป็นเพราะมีแรงมากระทำต่อวัตถุ กาลิเลโอได้ทำการทดลอง ณ หอเอนแห่งเมืองปิซา เพื่อพิสูจน์ให้เห็นว่า วัตถุต่างขนาดตกลงสู่พื้นโลกโดยใช้เวลาเท่ากัน แนวความคิดนี้ถูกนำไปพัฒนาเป็นกฎแรงโน้มถ่วงโดย เซอร์ไอแซค นิวตัน นักคณิตศาสตร์ชาวอังกฤษในยุคต่อมา
ที่มา
http://www.lesa.biz/astronomy/cosmos/galileo
กลับไปที่เนื้อหา
กฎของเคปเลอร์
ภาพที่ 1 โจฮานเนส เคปเลอร์
หลังจากที่กาลิเลโอพิสูจน์ว่า ระบบดวงอาทิตย์เป็นศูนย์กลางของระบบสุริยะ (Heliocentric) เป็นความจริง นักวิทยาศาสตร์ส่วนใหญ่ยังปักใจว่า วงโคจรของดาวเคราะห์เป็นรูปวงกลมที่สมบูรณ์ จึงไม่มีใครสามารถพยากรณ์ตำแหน่งของดาวเคราะห์ล่วงหน้าได้ถูกต้อง จนกระทั่ง โจฮานเนส เคปเลอร์ (Johannes Kepler) นักคณิตศาสตร์ชาวเยอรมันซึ่งมีชีวิตอยู่ในระหว่าง ค.ศ. 1571 – 1630 (พ.ศ. 2114 - 2173) ได้ทำการวิเคราะห์ข้อมูลตำแหน่งของดาวเคราะห์ ซึ่งได้มาจากการตรวจวัดอย่างละเอียดโดย ไทโค บราเฮ (Tycho Brahe) นักดาราศาสตร์ประจำราชสำนักเดนมาร์ก ผู้มีชื่อเสียงในยุคนั้น (แต่ไทโคคงยังเชื่อในระบบโลกเป็นศูนย์กลาง) แล้วทำการทดลองด้วยแบบจำลองทางคณิตศาสตร์ เคปเลอร์พบว่า ผลของการคำนวณซึ่งถือเอาวงโคจรของดาวเคราะห์เป็นรูปวงกลม ไม่สอดคล้องกับข้อมูลที่ได้จากการสังเกตการณ์ แต่สอดคล้องกับการคำนวณซึ่งถือเอาวงโคจรของดาวเคราะห์เป็นรูปวงรี ในปี ค.ศ. 1609 (พ.ศ. 2152) เคปเลอร์ได้ประกาศกฎข้อที่ 1 (กฎของวงรี) 'ดาวเคราะห์โคจรรอบดวงอาทิตย์เป็นวงรี โดยมีดวงอาทิตย์อยู่ที่โฟกัสจุดหนึ่ง'
ภาพที่ 2 วงโคจรของดาวเคราะห์เป็นวงรี
หมายเหตุ: การสร้างวงรี สามารถทำได้โดย 2 วิธีคือ วิธีขึงเชือก สร้างสามเหลี่ยมระหว่างจุดโฟกัส 2 จุดและปลายดินสอ จากนั้นลากดินสอรอบจุดโฟกัส โดยให้เส้นเชือกตรึงอยู่ตลอดเวลา ดังภาพที่ 3 และวิธีภาคตัดกรวย ในภาพที่ 4
ภาพที่ 3 การสร้างวงรี
ภาพที่ 4 ภาคตัดกรวยชนิดต่างๆ
ในปีเดียวกัน เคปเลอร์พบว่า ความเร็วในวงโคจรของดาวเคราะห์มิใช่ค่าคงที่ ดาวเคราะห์เคลื่อนที่เร็วขึ้นเมื่อเข้าใกล้ดวงอาทิตย์ และดาวเคราะห์จะเคลื่อนที่ช้าลงเมื่อออกห่างจากดวงอาทิตย์ เคปเลอร์ประกาศกฎข้อที่ 2 (กฎของพื้นที่เท่ากัน) “เมื่อดาวเคราะห์เคลื่อนที่ตามวงโคจรไปในแต่ละช่วงเวลา 1 หน่วย เส้นสมมติที่ลากโยงระหว่างดาวเคราะห์กับดวงอาทิตย์ จะกวาดพื้นที่ในอวกาศได้เท่ากัน”
ภาพที่ 5 พื้นที่ที่กวาดไปช่วงเวลาที่เท่ากัน ย่อมมีขนาดเท่ากัน
เก้าปีต่อมา ในปี ค.ศ. 1618 (พ.ศ. 2161) เคปเลอร์พบว่า พื้นที่ของคาบวงโคจรของดาวเคราะห์ (คำว่า 'พื้นที่' หมายถึง กำลังสอง) จะแปรผันตามปริมาตรของระยะห่างจากดวงอาทิตย์เสมอ (คำว่า 'ปริมาตร' หมายถึง กำลังสาม) หรือพูดอย่างง่ายว่า กำลังสองของคาบวงโคจรของดาวเคราะห์รอบดวงอาทิตย์ จะแปรผันตามกำลังสามของระยะห่างจากดวงอาทิตย์ เมื่อนำค่ายกกำลังสองของคาบวงโคจรของดาวเคราะห์ p2 มาหารด้วยค่ากำลังสามของระยะห่างจากดวงอาทิตย์ a3 จะได้ค่าคงที่เสมอ (p2 / a3 = k, k เป็นค่าคงที่) มิว่าจะเป็นดาวเคราะห์ดวงใดก็ตาม กฎข้อที่ 3 นี้เรียกว่า 'กฎฮาร์มอนิก' (Harmonic Law)
ตารางที่ 1 กฏข้อที่ 3 ของเคปเลอร์
|
คาบการโคจรรอบ |
ระยะห่างจาก |
กฏข้อที่ 3 |
|||
|
p |
p2 |
a |
a3 |
p2/a3 |
|
|
ดาวพุธ |
0.24 |
0.06 |
0.39 |
0.06 |
0.97 |
|
ดาวศุกร์ |
0.62 |
0.38 |
0.72 |
0.37 |
1.03 |
|
โลก |
1 |
1.00 |
1.00 |
1.00 |
1.00 |
|
ดาวอังคาร |
1.9 |
3.61 |
1.52 |
3.51 |
1.03 |
|
ดาวพฤหัสบดี |
12 |
144 |
5.20 |
140.61 |
1.02 |
|
ดาวเสาร์ |
29 |
841 |
9.50 |
857.38 |
0.98 |
|
ดาวยูเรนัส |
84 |
7,056 |
19.20 |
7,077.89 |
1.00 |
|
ดาวเนปจูน |
164 |
26,896 |
30.07 |
28,189.44 |
0.99 |
|
ดาวพลูโต |
248 |
61,504 |
39.72 |
62,655.39 |
0.98 |
โดยที่ระยะ ทาง 1 หน่วยดาราศาสตร์ หรือ 1 AU (Astronomical Unit) เท่ากับ ระยะทางเฉลี่ยจากโลกไปยังดวงอาทิตย์ หรือ 149,600,000 กิโลเมตร (ในยุคของเคปเลอร์ยังไม่ทราบว่า 1 AU มีค่าเท่าไร จึงติดค่าไ่ว้ในลักษณะของสัดส่วน)
อนึ่ง ในยุคของเคปเลอร์เป็นยุคที่เรขาคณิตรุ่งเรือง เคปเลอร์ได้สร้างแบบจำลองของระบบสุริยะแบบสามมิติ เป็นรูปทรงหลายเหลี่ยมซ้อนกันดังในภาพที่ 6 โดยถือว่า p2 คือพื้นที่ของเวลา และ a3 คือลูกบาศก์ของเวลา เป็นสัดส่วนกันในแต่ละชั้น
ภาพที่ 6 แบบจำลองระบบสุริยะของเคปเลอร์
สรุป กฎของเคปเลอร์
กฎข้อที่ 1: ดาวเคราะห์โคจรรอบดวงอาทิตย์เป็นวงรี โดยมีดวงอาทิตย์อยู่ที่โฟกัสจุดหนึ่ง
กฎข้อที่ 2: เวลาที่ดาวเคราะห์ใช้โคจรรอบดวงอาทิตย์ คาบเวลาเท่ากันจะกวาดได้พื้นที่เท่ากัน
กฎข้อที่ 3: กำลังสองของคาบวงโคจรรอบดวงอาทิตย์ แปรผันตามกำลังสามของระยะห่างจากดวงอาทิตย์ (p2 / a3 = k, k เป็นค่าคงที่)
ที่มา
http://www.lesa.biz/astronomy/cosmos/kepler
กลับไปที่เนื้อหา
กฎความโน้มถ่วงของนิวตัน
เซอร์ ไอแซค นิวตัน (Sir Isaac Newton) นักฟิสิกส์และคณิตศาสตร์ชาวอังกฤษถือกำเนิดใน ปี ค.ศ. 1642 (พ.ศ. 2185) นิวตัน สนใจดาราศาสตร์ และประดิษฐ์กล้องโทรทรรศน์แบบสะท้อนแสง (Reflecting telescope) ขึ้นโดยใช้โลหะเงาเว้าในการรวมแสงแทนการใช้เลนส์ในกล้องโทรทรรศน์แบบหักเหแสง (Refracting telescope) นิวตันติดใจในปริศนาที่ว่า แรงอะไรทำให้ผลแอปเปิลตกสู่พื้นดินและตรึงดวงจันทร์ไว้กับโลก สิ่งนี้เองนำเขาไปสู่การค้นพบกฎแรงโน้มถ่วง
เซอร์ ไอแซค นิวตัน (Sir Isaac Newton)
https://sites.google.com/site/
นิวตันได้เขียนถึงกฎการดึงดูดระหว่าง วัตถุ 2 วัตถุขึ้น เรียกว่ากฎของแรงโน้มถ่วงระหว่างกันของนิวตัน (Newton's Law of Gravitational Attraction) โดยเขาเชื่อว่า การที่ดาวเคราะห์เคลื่อนที่รอบดวงอาทิตย์เนื่องจากแรงกระทำระหว่างดวงอาทิตย์และดาวเคราะห์ โดยเป็นแรงดึงดูดระหว่างมวลเป็นแรงธรรมชาติที่จะดึงดูดวัตถุทุกชนิดที่มีมวล เขาจึงได้เสนอกฎแรงดึงดูดระหว่างมวล มีใจความว่า
"วัตถุทั้งหลายในเอกภพจะมีแรงดึงดูดซึ่งกันและกัน โดยขนาดของแรงดึงดูดระหว่างมวลคู่หนึ่งๆ จะแปรผันตรงกับผลคูณระหว่างมวลของวัตถุทั้งสอง และแปรผกผันกับกำลังสองของระยะทางระหว่างวัตถุทั้งสอง"
ซึ่งกฎนี้กำหนดให้มวลสองมวลใด ๆ จะต้องมีแรงดึงดูดระหว่างกันและกันเสมอ อย่างไรก็ตามเมื่อวัตถุต่างๆ อยู่บนผิวโลก แรงดึงดูดที่มีขนาดมากพอและมีผลกระทบต่อวัตถุต่างๆ จะมีเฉพาะแรงดึงดูดที่โลกกระทำกับวัตถุต่างๆ เท่านั้น ส่วนแรงระหว่างวัตถุด้วยกันมีค่าน้อยมาก เนื่องจากมวลของวัตถุเหล่านั้นน้อยมากเมื่อเทียบกับมวลของโลก
ตัวอย่าง เมื่อระยะทางระหว่างวัตถุเพิ่มขึ้น 2 เท่า แรงดึงดูดระหว่างวัตถุจะลดลง 4 เท่า เขาอธิบายว่า การร่วงหล่นของผลแอปเปิล ก็เช่นเดียวกับการร่วงหล่นของดวงจันทร์ ณ ตำแหน่งบนพื้นผิวโลก สมมติว่าแรงโน้มถ่วงบนพื้นผิวโลกมีค่า = 1 ระยะทางจากโลกถึงดวงจันทร์มีค่า 60 เท่าของรัศมีโลก ดังนั้นแรงโน้มถ่วง ณ ตำแหน่งวงโคจรของดวงจันทร์ย่อมมีค่าลดลง = 602 = 3,600 เท่า
 การเคลื่อนที่ในอวกาศ
การเคลื่อนที่ในอวกาศ
http://www.lesa.biz/astronomy/cosmos/planet-definition
ในภาพข้างล่าง แสดงให้เห็นว่า ใน 1 วินาที ดวงจันทร์เคลื่อนที่ไปได้ 1 กิโลเมตร จะถูกโลกดึงดูดให้ตกลงมา 1.4 มิลลิเมตร เมื่อดวงจันทร์โคจรไปได้ 1 เดือน ทั้งแรงตั้งต้นของดวงจันทร์ และแรงโน้มถ่วงของโลก ก็จะทำให้ดวงจันทร์โคจรได้ 1 รอบพอดี เราเรียกการตกเช่นนี้ว่า 'การตกแบบอิสระ' (Free fall) อันเป็นหลักการซึ่งมนุษย์นำไปประยุกต์ใช้กับการส่งยานอวกาศ และดาวเทียม ในยุคต่อมา

การเคลื่อนที่ของดวงจันทร์
http://portal.edu.chula.ac.th/lesa_cd/assets/document/lesa212/2/law_orbit/newton/newton.html
ตอนที่เคปเลอร์ค้นพบกฎการเคลื่อนที่ของดาวเคราะห์ ซึ่งได้จากผลของการสังเกตการณ์ในคริสต์ศตวรรษที่ 16 นั้น เขาไม่สามารถอธิบายว่าเหตุใดจึงเป็นเช่นนั้น จวบจนอีกหนึ่งศตวรรษต่อมา นิวตันได้ใช้กฎการแปรผกผันยกกำลังสอง อธิบายเรื่องการเคลื่อนที่ของดาวเคราะห์ ตามกฎทั้งสามข้อของเคปเลอร์ ดังนี้
• ดาวเคราะห์โคจรรอบดวงอาทิตย์เป็นรูปวงรี เกี่ยวเนื่องจากระยะทางและแรงโน้มถ่วงจากดวงอาทิตย์
• ในวงโคจรรูปวงรี ดาวเคราะห์จะเคลื่อนที่เร็ว ณ ตำแหน่งใกล้ดวงอาทิตย์ และดาวเคราะห์จะเคลื่อนที่ช้า ณ ตำแหน่งไกลจากดวงอาทิตย์ เนื่องจากอิทธิพลของระยะห่างระหว่างดวงอาทิตย์กับดาวเคราะห์
• ดาวเคราะห์ดวงในเคลื่อนที่ได้เร็วกว่าดาวเคราะห์ดวงนอก เป็นเพราะว่าอยู่ใกล้กับดวงอาทิตย์มากกว่า จึงมีแรงโน้มถ่วงระหว่างกันมากกว่า
เรียบเรียงจาก
http://www.atom.rmutphysics.com/charud/scibook/dynamic1/index6_2.html
www.myfirstbrain.com/student_view.aspx?id=75481
http://portal.edu.chula.ac.th/lesa_cd/assets/document/lesa212/2/law_orbit/newton/newton.html
กลับไปที่เนื้อหา
-
7314 ดาวเคราะห์ (The Planets) /lesson-physics/item/7314-the-planetsเพิ่มในรายการโปรด